| Date | May 2013 | Marks available | 3 | Reference code | 13M.1.sl.TZ2.4 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Sketch | Question number | 4 | Adapted from | N/A |
Question
The diagram below shows the graph of a function \(f\) , for \( - 1 \le x \le 2\) .
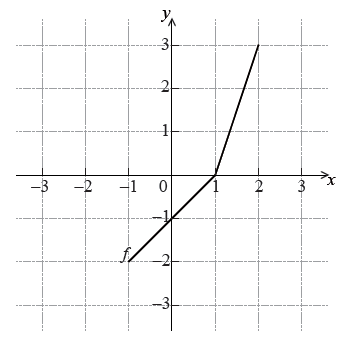
Write down the value of \(f(2)\).
Write down the value of \({f^{ - 1}}( - 1)\) .
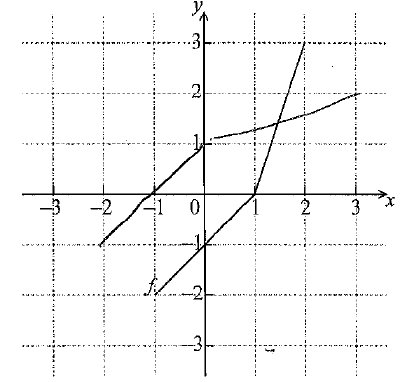
Sketch the graph of \({f^{ - 1}}\) on the grid below.
Markscheme
\(f(2) = 3\) A1 N1
[1 mark]
\({f^{ - 1}}( - 1) = 0\) A2 N2
[2 marks]
EITHER
attempt to draw \(y = x\) on grid (M1)
OR
attempt to reverse x and y coordinates (M1)
eg writing or plotting at least two of the points
\(( - 2, - 1)\) , \(( - 1,0)\) , \((0,1)\) , \((3,2)\)
THEN
correct graph A2 N3
[3 marks]
Examiners report
In part (a) of this question, most candidates were able to find the value of \(f(2)\) correctly, while some had trouble finding \({f^{ - 1}}( - 1)\). Many candidates tried to find an equation for the function, or to make tables of values to help them find their answers. The intent of this question was to read the answers from the given graph. Candidates should be reminded that when the command term is "write down", there is no need for them to do large amounts of working.
In part (b) of this question, candidates were generally successful in reversing the \(x\) and \(y\) coordinates of key points or reflecting in the \(y = x\) line to correctly sketch the graph of the inverse function. Common errors included not sketching the graph for the appropriate domain, or sketching the graph of \(f(-x)\) or the graph of \(-f(x)\).

