| Date | May 2015 | Marks available | 3 | Reference code | 15M.2.sl.TZ2.5 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
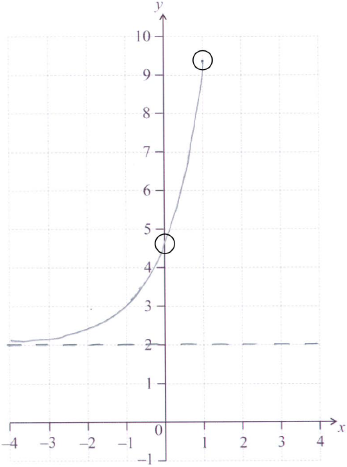
Let \(f(x) = {{\text{e}}^{x + 1}} + 2\), for \( - 4 \le x \le 1\).
On the following grid, sketch the graph of \(f\).
The graph of \(f\) is translated by the vector \(\left( {\begin{array}{*{20}{c}} 3 \\ { - 1} \end{array}} \right)\) to obtain the graph of a function \(g\).
Find an expression for \(g(x)\).
Markscheme
 1A1A1 N3
1A1A1 N3
Note: Curve must be approximately correct exponential shape (increasing and concave up). Only if the shape is approximately correct, award the following:
A1 for right end point in circle,
A1 for \(y\)-intercept in circle,
A1 for asymptotic to \(y = 2\), (must be above \(y = 2\)).
[3 marks]
valid attempt to find \(g\) (M1)
eg\(\;\;\;f(x - 3) - 1,{\text{ }}g(x) = {{\text{e}}^{x + 1 - 3}} + 2 - 1,{\text{ }}{{\text{e}}^{x + 1 - 3}},{\text{ }}2 - 1\), sketch
\(g(x) = {{\text{e}}^{x - 2}} + 1\) A2 N3
[3 marks]
Total [6 marks]
Examiners report
Although this question involved a straightforward use of the GDC, the graphing of this exponential function on a given grid seemed challenging for a number of candidates. Although most candidates were able to graph the correct shape, they did not take into account the domain and range of this function.
Many were inattentive to the asymptotic nature of the function. Very few actually drew the asymptote, which in this case was a relevant feature.
When finding an expression for \(g\), many reversed the direction of one or both of the transformations. The vertical translation was usually correct, but the horizontal shift was poorly done. The most common error was to obtain \(g(x) = {{\text{e}}^{x + 4}} + 1\).
Although this question involved a straightforward use of the GDC, the graphing of this exponential function on a given grid seemed challenging for a number of candidates. Although most candidates were able to graph the correct shape, they did not take into account the domain and range of this function.
Many were inattentive to the asymptotic nature of the function. Very few actually drew the asymptote, which in this case was a relevant feature.
When finding an expression for \(g\), many reversed the direction of one or both of the transformations. The vertical translation was usually correct, but the horizontal shift was poorly done. The most common error was to obtain \(g(x) = {{\text{e}}^{x + 4}} + 1\).

