 In the Cosmology and Age of the universe SL pages we considered cosmological observations and how these act as evidence for the origin and evolution of the universe in the past. Now we will instead look forwards to the future of the universe.
In the Cosmology and Age of the universe SL pages we considered cosmological observations and how these act as evidence for the origin and evolution of the universe in the past. Now we will instead look forwards to the future of the universe.
Key Concepts
The cosmological principle
The cosmological principle states that the spatial distribution of matter in the universe is homogeneous (consistent physical properties at any observer's location) and isotropic (consistent physical properties when observed in any direction) when viewed on a large enough scale. This assumes that forces act uniformly throughout the universe and that there are no irregularities in the matter that was initially laid down by the Big Bang.

We will return to cosmological principle and its role when we consider critical density and models of the universe.
Fluctuations in the CMB
While StudyIB Physics geeks will know that we prefer to show the cosmic microwave background as being homogeneous and isotropic, students at AHL must also be prepared to discuss the observed anisotropies in the CMB.

There are three sets of results for you to get familiar with:
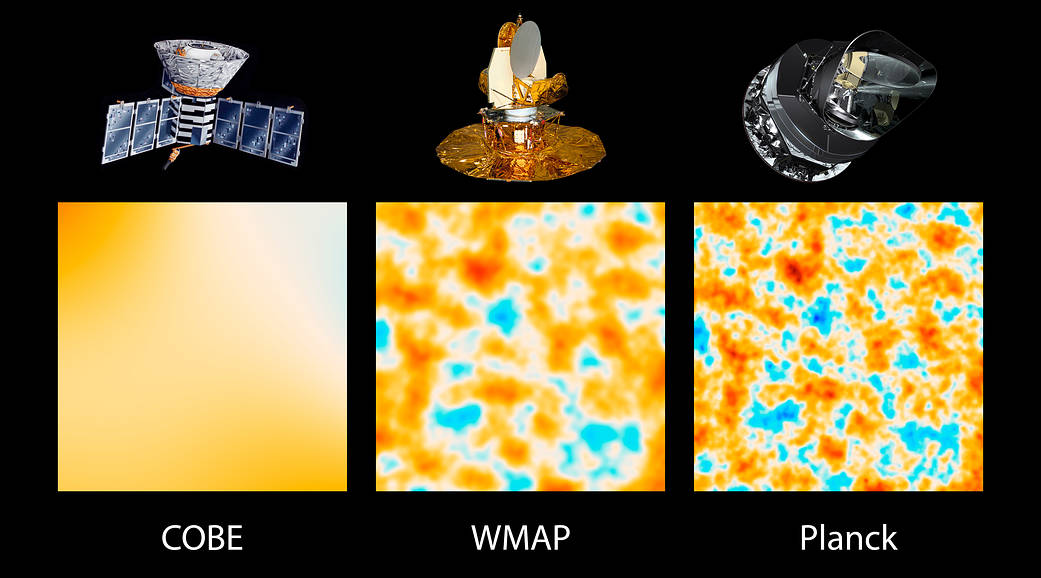
- COBE (NASA Cosmic Background Explorer launched 1989) - took precise measurements of the spectrum, the anisotropy of the radiation and the angular distribution of the diffuse radiation between 1 μm and 1 cm over the whole celestial sphere. The variations in the light are indicative of clusters of galaxies and empty space. In mapping the oldest light in the universe, the Big Bang theory of the universe was confirmed.
- WMAP (NASA Wilkinson Microwave Anisotropy Probe launched June 2001) - improved the precision of the measurements to produce a map of higher resolution. Found evidence for inflation (the early rapid expansion of the universe), found the temperature of the cosmic background to be 2.7 K, determined the age of the universe and determined the proportions of matter, dark matter and dark energy.
- Planck space observatory (ESA launched 2009) - the most advanced satellite images the sky with more than 2.5 times greater resolution than WMAP. Reveals patterns in the cosmic background and created the sharpest all-sky map ever made of the universe's cosmic microwave background.
Cosmological origin of redshift
Where did the cosmic microwave background come from? The beginning of the universe!
When the universe was formed, it was densely packed with photons and fundamental particles. The temperature was too high for atom formation and so instead was radiation-dominated. As the universe has expanded, the photons have not disappeared but have instead stretched so that their wavelengths have converted from gamma to microwave radiation.
The anisotropies in the CMB images today show that the early universe was not perfectly uniform, which is why we have a contrast between galaxies and empty space. As the universe expanded and cooled, had the density been perfectly uniform, the gravitational attraction between all particles would have been balanced in all directions, so none would have come together.
Definition
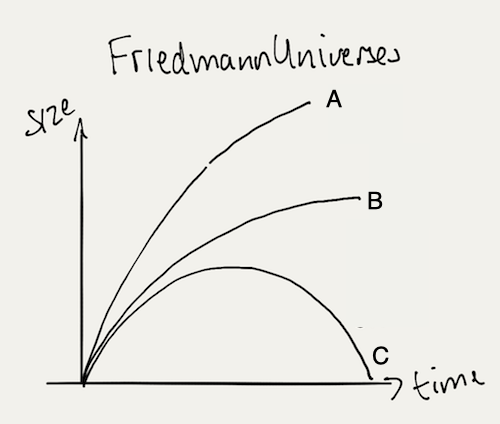
We know from Hubble's observations of receding galaxies that the universe continues to expand. We also know, however, that the universe is not infinite as an infinite universe would have an infinite number of stars and have existed for infinite time, meaning that the night sky would not be dark but instead bright in every direction. Therefore, there must be a net gravitational force acting between all of the galaxies. Is this strong enough to eventually stop the expansion and commence universal contraction?
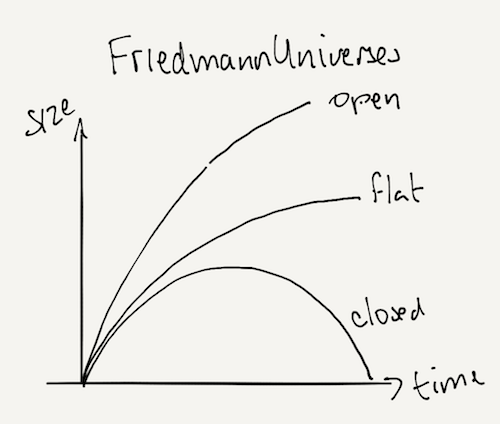
The tipping point is referred to as critical density:
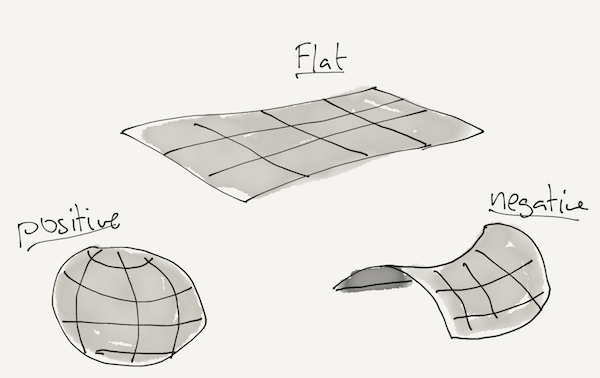
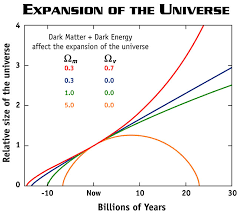
- If the density of the universe exceeds the critical density, the universe will stop expanding and contract. We call this a closed universe. This would lead to a 'big crunch'!
- If the density of the universe is equal to the critical density, the rate of expansion of the universe would tend towards zero as time tends towards infinity. The universe is considered flat.
- If the density of the universe is less than the critical density, the universe will expand forever; an open universe.
Derivation
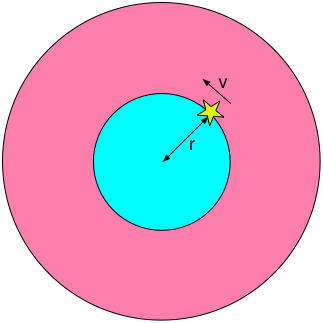
We can derive this critical density from Newtonian gravitation.
If the universe has critical density, a mass at the edge of the expanding universe would have all of its kinetic energy be converted into potential energy at infinity.

- At present, its kinetic energy is \({1\over 2}mv^2\) and its potential energy is \(-GMm\over r\)
- At infinity, its kinetic energy and its potential energy are zero (by definition)
- According to conservation of energy: \({1\over 2}mv^2-{GMm\over r}=0\)
- The mass of the universe can be determined from the critical denisty: \(M={4\over 3}\pi r^3\rho_c\)
- And we know from Hubble's law that \(v=H_0r\)
By combination, rearranging and substitution we can calculate a value for the critical density:
\(\rho_c={3{H_0}^2\over 8\pi G}\)
- \(\rho_c\) is the critical density of the universe (~10-26 kgm-3)
- \(H_0\) is the Hubble constant (=68 kms-1Mpc-1)
- \(G\) is the universal gravitational constant (6.67 × 10-11 m3kg-1s-2)
The critical density of approximately 10-26 kgm-3 is equivalent to 6 hydrogen atoms per cubic metre.
In this simulation you can see how the kinetic and potential energies vary as the cloud expands:
How much of AHL Further cosmology have you understood?


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn