| Date | November 2017 | Marks available | 2 | Reference code | 17N.2.SL.TZ0.T_6 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Show that | Question number | T_6 | Adapted from | N/A |
Question
A restaurant serves desserts in glasses in the shape of a cone and in the shape of a hemisphere. The diameter of a cone shaped glass is 7.2 cm and the height of the cone is 11.8 cm as shown.
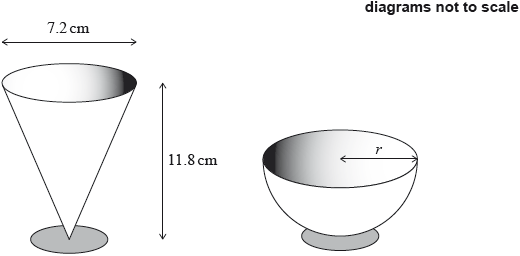
The volume of a hemisphere shaped glass is .
The restaurant offers two types of dessert.
The regular dessert is a hemisphere shaped glass completely filled with chocolate mousse. The cost, to the restaurant, of the chocolate mousse for one regular dessert is $1.89.
The special dessert is a cone shaped glass filled with two ingredients. It is first filled with orange paste to half of its height and then with chocolate mousse for the remaining volume.
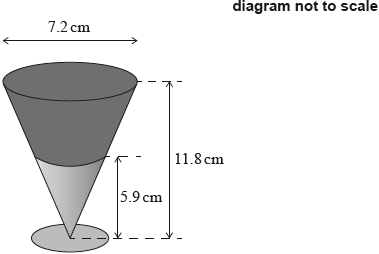
The cost, to the restaurant, of of orange paste is $7.42.
A chef at the restaurant prepares 50 desserts; regular desserts and special desserts. The cost of the ingredients for the 50 desserts is $111.44.
Show that the volume of a cone shaped glass is , correct to 3 significant figures.
Calculate the radius, , of a hemisphere shaped glass.
Find the cost of of chocolate mousse.
Show that there is of orange paste in each special dessert.
Find the total cost of the ingredients of one special dessert.
Find the value of .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
Note: Award (M1) for correct substitution into volume of a cone formula.
(A1)
(AG)
Note: Both rounded and unrounded answers must be seen for the final (A1) to be awarded.
[2 marks]
(M1)(A1)
Notes: Award (M1) for multiplying volume of sphere formula by (or equivalent).
Award (A1) for equating the volume of hemisphere formula to 225.
OR
(A1)(M1)
Notes: Award (A1) for 450 seen, (M1) for equating the volume of sphere formula to 450.
(A1)(G2)
[3 marks]
(M1)
Note: Award (M1) for dividing 1.89 by 2.25, or equivalent.
(A1)(G2)
Note: Accept 84 cents if the units are explicit.
[2 marks]
(A1)
(M1)
Note: Award (M1) for correct substitution into volume of a cone formula, but only if the result rounds to 20.
(AG)
OR
(A1)
(M1)
Notes: Award (M1) for multiplying 160 by . Award (A0)(M1) for if is not seen.
(AG)
Notes: Do not award any marks if the response substitutes in the known value to find the radius of the cone.
[2 marks]
(M1)
Note: Award (M1) for the sum of two correct products.
$ 2.66 (A1)(ft)(G2)
Note: Follow through from part (c).
[2 marks]
(M1)
Note: Award (M1) for correct equation.
(M1)
Note: Award (M1) for setting up correct equation, including their 2.66 from part (e).
(A1)(ft)(G3)
Note: Follow through from part (e), but only if their answer for is rounded to the nearest positive integer, where .
Award at most (M1)(M1)(A0) for a final answer of “28, 22”, where the -value is not clearly defined.
[3 marks]

