| Date | November 2017 | Marks available | 1 | Reference code | 17N.1.AHL.TZ0.H_9 |
| Level | Additional Higher Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Find | Question number | H_9 | Adapted from | N/A |
Question
In the following diagram, = a, = b. C is the midpoint of [OA] and .
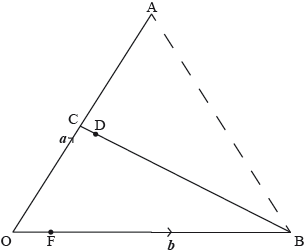
It is given also that and , where .
Find, in terms of a and b .
Find, in terms of a and b .
Find an expression for in terms of a, b and ;
Find an expression for in terms of a, b and .
Show that , and find the value of .
Deduce an expression for in terms of a and b only.
Given that area , find the value of .
Markscheme
b A1
[1 mark]
(M1)
b – a A1
[2 marks]
a M1A1
[2 marks]
a M1A1
[2 marks]
equating coefficients: M1
A1
solving simultaneously: M1
A1AG
[4 marks]
M1A1
[2 marks]
METHOD 1
(M1)
(M1)
A1
(M1)
A1
METHOD 2
A1
or M1
(M1)
A1
A1
[5 marks]

