IB Questionbank

User interface language: English | Español

Date	May 2018	Marks available	1	Reference code	18M.3.SL.TZ1.6
Level	Standard level	Paper	Paper 3	Time zone	1
Command term	Calculate	Question number	6	Adapted from	N/A

Question

A constant force of 50.0 N is applied tangentially to the outer edge of a merry-go-round. The following diagram shows the view from above.

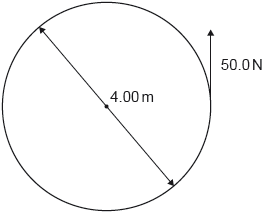
M18/4/PHYSI/SP3/ENG/TZ1/06

The merry-go-round has a moment of inertia of 450 kg m² about a vertical axis. The merry-go-round has a diameter of 4.00 m.

A child of mass 30.0 kg is now placed onto the edge of the merry-go-round. No external torque acts on the system.

The child now moves towards the centre.

The merry-go-round starts from rest and the force is applied for one complete revolution.

Show that the angular acceleration of the merry-go-round is 0.2 rad s^–2.

[2]

Calculate, for the merry-go-round after one revolution, the angular speed.

[1]

b.i.

Calculate, for the merry-go-round after one revolution, the angular momentum.

[1]

b.ii.

Calculate the new angular speed of the rotating system.

[2]

Explain why the angular speed will increase.

[2]

d.i.

Calculate the work done by the child in moving from the edge to the centre.

[2]

d.ii.

Markscheme

Γ «= Fr = 50 × 2» = 100 «Nm»

α « $= \frac{\Gamma }{I} = \frac{{100}}{{450}}$ » =0.22 «rads^–2»

Final value to at least 2 sig figs, OR clear working with substitution required for mark.

[2 marks]

« $\omega _t^2 - \omega _0^2 = 2\alpha \Delta \theta$ »

« $\omega _t^2 - 0 = 2 \times 0.22 \times 2\pi$ »

${\omega _t} = 1.7$ «rads^–1»

Accept BCA, values in the range: 1.57 to 1.70.

[1 mark]

b.i.

«L = Iω = 450 × 1.66»

= 750 «kgm² rads^–1»

Accept BCA, values in the range: 710 to 780.

[1 mark]

b.ii.

«I = 450 + mr²»

I «= 450 + 30 × 2²» = 570 «kgm²»

«L = 570 × ω = 747»

ω = 1.3 «rads^–1»

Watch for ECF from (a) and (b).

Accept BCA, values in the range: 1.25 to 1.35.

[2 marks]

moment of inertia will decrease

angular momentum will be constant «as the system is isolated»

«so the angular speed will increase»

[2 marks]

d.i.

ω_t = 1.66 from bi AND W = ΔE_k

W = $\frac{1}{2}$ × 450 × 1.66² – $\frac{1}{2}$ × 570 × 1.31² = 131 «J»

ECF from 8bi

Accept BCA, value depends on the answers in previous questions.

[2 marks]

d.ii.

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

d.i.

[N/A]

d.ii.

Syllabus sections

Option B: Engineering physics » Option B: Engineering physics (Core topics) » B.1 – Rigid bodies and rotational dynamics

Show 52 related questions

17M.3.SL.TZ2.6c.i:
Determine the final angular speed of the probe–satellite system.
18M.3.SL.TZ1.6d.i:
Explain why the angular speed will increase.
16N.3.SL.TZ0.9: The diagram shows two methods of pedalling a bicycle using a force F. In method 1 the...
18M.3.SL.TZ2.6a.iii:
Determine the angular velocity of the wheel at B.
18M.3.SL.TZ2.6b.ii:
Describe the effect of F on the angular speed of the wheel.
18N.3.SL.TZ0.6b.ii:
After time t the rod makes an angle θ with the horizontal. Outline why the equation $\theta = \frac{1}{2}\alpha {t^2}$ cannot be used to find the time it takes θ to become $\frac{\pi }{2}$ (that is for the rod to become vertical for the first time).
18N.3.SL.TZ0.6c.ii: At the instant the rod becomes vertical calculate the angular momentum of the rod.
18N.3.SL.TZ0.6a: Calculate the force the support exerts on the rod.
18M.3.SL.TZ2.6a.ii:
In moving from point A to point B, the centre of mass of the wheel falls through a vertical distance of 0.36 m. Show that the translational speed of the wheel is about 1 m s^–1 after its displacement.
17N.3.SL.TZ0.7c: Calculate the acceleration of the hoop when θ = 20°. Assume that the hoop continues to roll...
17M.3.SL.TZ2.6a.i:
Deduce the linear acceleration of the centre of mass of the probe.
16N.3.SL.TZ0.8a:
The velocity of the falling object is 1.89 m s^–1 at 3.98 s. Calculate the average angular acceleration of the flywheel.
18N.3.SL.TZ0.6c.i:
At the instant the rod becomes vertical show that the angular speed is ω = 2.43 rad s^–1.
18N.3.SL.TZ0.6b.i:
Calculate, in rad s^–2, the initial angular acceleration $\alpha$ of the rod.
17N.3.SL.TZ0.6a: Explain what is meant by proper length.
17N.3.SL.TZ0.7a: On the diagram, draw and label the forces acting on the hoop.
19N.3.SL.TZ0.5b(ii): Show that the angular velocity of the flywheel at t = 5.00 s is 200 rad s–1.
19N.3.SL.TZ0.5a: State the torque provided by the force W about the axis of the flywheel.
19N.3.SL.TZ0.5b(iii):
Calculate the maximum tension in the string.
19N.3.SL.TZ0.5c(i): The flywheel is in translational equilibrium. Distinguish between translational equilibrium...
19N.3.SL.TZ0.5b(i): Identify the physical quantity represented by the area under the graph.
17N.3.SL.TZ0.7d:
State the relationship between the force of friction and the angle of the incline.
16N.3.SL.TZ0.8b:
Show that the torque acting on the flywheel is about 0.3 Nm.
17M.3.SL.TZ1.5b.ii:
Calculate the number of revolutions made by the system before it comes to rest.
18M.3.SL.TZ2.6a.i:
The moment of inertia of the wheel is 1.3 × 10^–4 kg m². Outline what is meant by the moment of inertia.
18M.3.SL.TZ1.6c:
Calculate the new angular speed of the rotating system.
19M.3.SL.TZ2.8b:
Calculate F.
18M.3.SL.TZ1.6b.i:
Calculate, for the merry-go-round after one revolution, the angular speed.
20N.3.SL.TZ0.6a:
Show that the final angular velocity of the bar is about $3 rad s^{- 1}$ .
16N.3.SL.TZ0.8c:
(i) Calculate the tension in the string.

(ii) Determine the mass m of the falling object.
17N.3.SL.TZ0.7e:
The angle of the incline is slowly increased from zero. Determine the angle, in terms of the coefficient of friction, at which the hoop will begin to slip.
19N.3.SL.TZ0.5c(ii):
At t = 5.00 s the flywheel is spinning with angular velocity 200 rad s^–1. The support bearings exert a constant frictional torque on the axle. The flywheel comes to rest after 8.00 × 10³ revolutions. Calculate the magnitude of the frictional torque exerted on the flywheel.
19M.3.SL.TZ2.9a:
Show that the total kinetic energy E_k of the sphere when it rolls, without slipping, at speed v is ${E_{\text{K}}} = \frac{7}{{10}}m{v^2}$ .
20N.3.SL.TZ0.6d:
The torque is removed. The bar comes to rest in $30$ complete rotations with constant angular deceleration. Determine the time taken for the bar to come to rest.
20N.3.SL.TZ0.6b:
Draw the variation with time $t$ of the angular displacement $θ$ of the bar during the acceleration.
20N.3.SL.TZ0.7b: Explain the changes to the rotational kinetic energy in the person-turntable system.
20N.3.SL.TZ0.7a:
Explain the direction in which the person-turntable system starts to rotate.
20N.3.SL.TZ0.6c:
Calculate the torque acting on the bar while it is accelerating.
20N.3.SL.TZ0.8:
A solid sphere of radius $r$ and mass $m$ is released from rest and rolls down a slope, without slipping. The vertical height of the slope is $h$ . The moment of inertia $I$ of this sphere about an axis through its centre is $\frac{2}{5} m r^{2}$ .

Show that the linear velocity $v$ of the sphere as it leaves the slope is $\sqrt{\frac{10 g h}{7}}$ .
17M.3.SL.TZ2.6b:
The forces act for 2.00 s. Show that the final angular speed of the probe is about 16 rad $\,$ s^–1.
17N.3.SL.TZ0.7b:
Show that the linear acceleration a of the hoop is given by the equation shown.

a = $\frac{{g \times \sin q}}{2}$
18M.3.SL.TZ1.6d.ii:
Calculate the work done by the child in moving from the edge to the centre.
19M.3.SL.TZ2.8a: Outline why the normal force acting on the ladder at the point of contact with the wall is...
17M.3.SL.TZ1.5a.i:
Write down an expression, in terms of M, v and R, for the angular momentum of the system about the vertical axis just before the collision.
17M.3.SL.TZ1.5a.ii:
Just after the collision the system begins to rotate about the vertical axis with angular velocity ω. Show that the angular momentum of the system is equal to $\frac{4}{3}M{R^2}\omega$ .
17M.3.SL.TZ1.5a.iii:
Hence, show that $\omega = \frac{v}{{4R}}$ .
17M.3.SL.TZ1.5b.i:
Show that the angular deceleration of the system is 0.043 rad $\,$ s^–2.
17M.3.SL.TZ2.6a.ii:
Calculate the resultant torque about the axis of the probe.
17M.3.SL.TZ1.5a.iv:
Determine in terms of M and v the energy lost during the collision.
17M.3.SL.TZ2.6c.ii:
Calculate the loss of rotational kinetic energy due to the linking of the probe with the satellite.
18M.3.SL.TZ1.6a:
Show that the angular acceleration of the merry-go-round is 0.2 rad s^–2.
19M.3.SL.TZ2.9b:
A solid sphere of mass 1.5 kg is rolling, without slipping, on a horizontal surface with a speed of 0.50 m s^-1. The sphere then rolls, without slipping, down a ramp to reach a horizontal surface that is 45 cm lower.

Calculate the speed of the sphere at the bottom of the ramp.

Hide related questions

Option B: Engineering physics » Option B: Engineering physics (Core topics)

Option B: Engineering physics

Question

Markscheme

Examiners report

Syllabus sections

View options