| Date | November 2013 | Marks available | 10 | Reference code | 13N.3sp.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Statistics and probability | Time zone | TZ0 |
| Command term | Decide, State, and Apply | Question number | 4 | Adapted from | N/A |
Question
Francisco and his friends want to test whether performance in running 400 metres improves if they follow a particular training schedule. The competitors are tested before and after the training schedule.
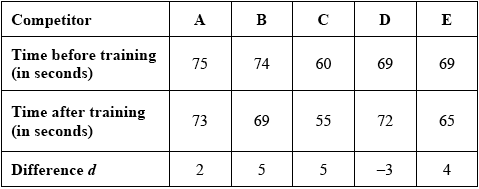
The times taken to run 400 metres, in seconds, before and after training are shown in the following table.

Apply an appropriate test at the 1% significance level to decide whether the training schedule improves competitors’ times, stating clearly the null and alternative hypotheses. (It may be assumed that the distributions of the times before and after training are normal.)
Markscheme
\({{\text{H}}_0}\): the training schedule does not help improve times (or \(\mu = 0\)) A1
\({{\text{H}}_1}\): the training schedule does help improve times (or \(\mu > 0\)) A1
Note: Subsequent marks can be awarded even if the hypotheses are not stated.
(Assuming difference of times is normally distributed.)
let \(d{\text{ time before training }}-{\text{ time after training}}\) (M1)
EITHER
\(n = 5,{\text{ }}\sum {d = 13,{\text{ }}} \sum {{d^2} = 79 \Rightarrow s_{n - 1}^2 = \frac{1}{4}\left( {79 - \frac{{169}}{5}} \right) = 11.3} \) (M1)
(small sample) so use a one-sided t-test (M1)
Note: The “one-sided” t-test may have been seen above when stating \({{\text{H}}_1}\).
\(t = \frac{{2.6}}{{\sqrt {\frac{{11.3}}{5}} }} = 1.7 \ldots \) A1
\(v = 4\), A1
at the 1% level the critical value is 3.7 A1
since \({\text{3.7}} > {\text{1.7}} \ldots \)
\({{\text{H}}_0}\) is accepted (insufficient evidence to reject \({{\text{H}}_0}\)) R1
Note: Follow through their t-value.
OR
(small sample) so use a one-sided t-test (M1)
\(p = 0.079 \ldots \) A4
since \(0.079 \ldots > 0.01\)
\({{\text{H}}_0}\) is accepted (insufficient evidence to reject \({{\text{H}}_0}\)) R1
Note: Follow through their p-value.
Note: Accept \(d = {\text{time after training }}-{\text{ time before training throughout}}\).
[10 marks]
Examiners report
It was again disappointing to see many candidates giving incorrect hypotheses. A common error was to give the hypotheses the wrong way around. Candidates should be aware that in this type of problem the null hypothesis always represents the status quo. Also, some candidates defined ‘\(d = {\text{time before }}-{\text{ time after}}\)’ and then gave the hypotheses incorrectly as \({{\text{H}}_0}:d = 0\) or \(\bar d = 0;{\text{ }}{{\text{H}}_1}:d > 0\) or \(\bar d > 0\). It is important to note that the parameter being tested here is \(E(d)\) or \({\mu _d}\) although \(\mu \) was accepted.

