| Date | November 2013 | Marks available | 2 | Reference code | 13N.3sp.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Statistics and probability | Time zone | TZ0 |
| Command term | Explain | Question number | 1 | Adapted from | N/A |
Question
A traffic radar records the speed, \(v\) kilometres per hour (\({\text{km}}\,{{\text{h}}^{-{\text{1}}}}\)), of cars on a section of a road.
The following table shows a summary of the results for a random sample of 1000 cars whose speeds were recorded on a given day.
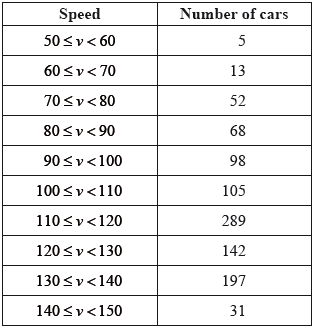
Using the data in the table,
(i) show that an estimate of the mean speed of the sample is 113.21 \({\text{km}}\,{{\text{h}}^{-{\text{1}}}}\);
(ii) find an estimate of the variance of the speed of the cars on this section of the road.
Find the 95% confidence interval, \(I\), for the mean speed.
Let \(J\) be the 90% confidence interval for the mean speed.
Without calculating \(J\), explain why \(J \subset I\).
Markscheme
(i) \(\bar v = \frac{1}{{1000}}(55 \times 5 + 65 \times 13 + \ldots + 145 \times 31)\) A1M1
Note: A1 for mid-points, M1 for use of the formula.
\( = \frac{{113\,210}}{{1000}} = 113.21\) AG
(ii) \({s^2} = \frac{{{{(55 - 113.21)}^2} \times 5 + {{(65 - 113.21)}^2} \times 13 + \ldots + {{(145 - 113.21)}^2} \times 31}}{{999}}\) (M1)
\( = \frac{{362\,295.9}}{{999}} = 362.6585 \ldots = 363\) A1
Note: Award A1 if answer rounds to 362 or 363.
Note: Condone division by 1000.
[4 marks]
\(\bar v \pm \frac{{{t_{0.025}} \times s}}{{\sqrt n }}\) (M1)
hence the confidence interval \(I = [112.028,{\text{ }}114.392]\) A1
Note: Accept answers which round to 112 and 114.
Note: Condone the use of \({z_{0.025}}\) for \({t_{0.025}}\) and \(\sigma \) for \(s\).
[2 marks]
less confidence implies narrower interval R2
Note: Accept equivalent statements or arguments having a meaningful diagram and/or relevant percentiles.
hence the confidence interval \(I\) at the 95% level contains the confidence interval \(J\) at the 90% level AG
[2 marks]
Examiners report
In (a)(i), the candidates were required to show that the estimate of the mean is 113.21 so that those who stated simply ‘Using my GDC, mean = 113.21’ were given no credit. Candidates were expected to indicate that the interval midpoints were used and to show the appropriate formula. In (a)(ii), division by either 999 or 1000 was accepted, partly because of the large sample size and partly because the question did not ask for an unbiased estimate of variance.
Solutions to (c) were often badly written, often quite difficult to understand exactly what was being stated.

