| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.hl.TZ2.14 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find, Hence, and State | Question number | 14 | Adapted from | N/A |
Question
Consider the following functions:
\(h(x) = \arctan (x),{\text{ }}x \in \mathbb{R}\)
\(g(x) = \frac{1}{x}\), \(x\in \mathbb{R}\), \({\text{ }}x \ne 0\)
Sketch the graph of \(y = h(x)\).
Find an expression for the composite function \(h \circ g(x)\) and state its domain.
Given that \(f(x) = h(x) + h \circ g(x)\),
(i) find \(f'(x)\) in simplified form;
(ii) show that \(f(x) = \frac{\pi }{2}\) for \(x > 0\).
Nigel states that \(f\) is an odd function and Tom argues that \(f\) is an even function.
(i) State who is correct and justify your answer.
(ii) Hence find the value of \(f(x)\) for \(x < 0\).
Markscheme
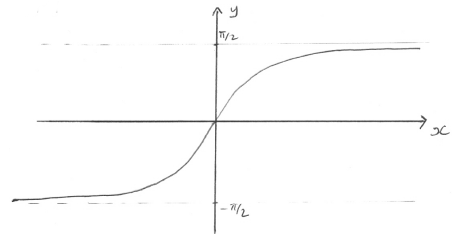 A1A1
A1A1
Note: A1 for correct shape, A1 for asymptotic behaviour at \(y = \pm \frac{\pi }{2}\).
[2 marks]
\(h \circ g(x) = \arctan \left( {\frac{1}{x}} \right)\) A1
domain of \(h \circ g\) is equal to the domain of \(g:x \in \circ ,{\text{ }}x \ne 0\) A1
[2 marks]
(i) \(f(x) = \arctan (x) + \arctan \left( {\frac{1}{x}} \right)\)
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{1}{{1 + \frac{1}{{{x^2}}}}} \times - \frac{1}{{{x^2}}}\) M1A1
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{{ - \frac{1}{{{x^2}}}}}{{\frac{{{x^2} + 1}}{{{x^2}}}}}\) (A1)
\( = \frac{1}{{1 + {x^2}}} - \frac{1}{{1 + {x^2}}}\)
\( = 0\) A1
(ii) METHOD 1
f is a constant R1
when \(x > 0\)
\(f(1) = \frac{\pi }{4} + \frac{\pi }{4}\) M1A1
\( = \frac{\pi }{2}\) AG
METHOD 2
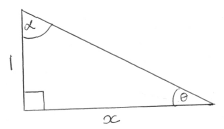
from diagram
\(\theta = \arctan \frac{1}{x}\) A1
\(\alpha = \arctan x\) A1
\(\theta + \alpha = \frac{\pi }{2}\) R1
hence \(f(x) = \frac{\pi }{2}\) AG
METHOD 3
\(\tan \left( {f(x)} \right) = \tan \left( {\arctan (x) + \arctan \left( {\frac{1}{x}} \right)} \right)\) M1
\( = \frac{{x + \frac{1}{x}}}{{1 - x\left( {\frac{1}{x}} \right)}}\) A1
denominator = 0, so \(f(x) = \frac{\pi }{2}{\text{ (for }}x > 0)\) R1
[7 marks]
(i) Nigel is correct. A1
METHOD 1
\(\arctan (x)\) is an odd function and \(\frac{1}{x}\) is an odd function
composition of two odd functions is an odd function and sum of two odd functions is an odd function R1
METHOD 2
\(f( - x) = \arctan ( - x) + \arctan \left( { - \frac{1}{x}} \right) = - \arctan (x) - \arctan \left( {\frac{1}{x}} \right) = - f(x)\)
therefore f is an odd function. R1
(ii) \(f(x) = - \frac{\pi }{2}\) A1
[3 marks]

