| Date | May 2014 | Marks available | 5 | Reference code | 14M.3ca.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Find and Show that | Question number | 2 | Adapted from | N/A |
Question
Consider the functions \(f(x) = {(\ln x)^2},{\text{ }}x > 1\) and \(g(x) = \ln \left( {f(x)} \right),{\text{ }}x > 1\).
(i) Find \(f'(x)\).
(ii) Find \(g'(x)\).
(iii) Hence, show that \(g(x)\) is increasing on \(\left] {1,{\text{ }}\infty } \right[\).
Consider the differential equation
\[(\ln x)\frac{{{\text{d}}y}}{{{\text{d}}x}} + \frac{2}{x}y = \frac{{2x - 1}}{{(\ln x)}},{\text{ }}x > 1.\]
(i) Find the general solution of the differential equation in the form \(y = h(x)\).
(ii) Show that the particular solution passing through the point with coordinates \(\left( {{\text{e, }}{{\text{e}}^2}} \right)\) is given by \(y = \frac{{{x^2} - x + {\text{e}}}}{{{{(\ln x)}^2}}}\).
(iii) Sketch the graph of your solution for \(x > 1\), clearly indicating any asymptotes and any maximum or minimum points.
Markscheme
(i) attempt at chain rule (M1)
\(f'(x) = \frac{{2\ln x}}{x}\) A1
(ii) attempt at chain rule (M1)
\(g'(x) = \frac{2}{{x\ln x}}\) A1
(iii) \(g'(x)\) is positive on \(\left] {1,{\text{ }}\infty } \right[\) A1
so \(g(x)\) is increasing on \(\left] {1,{\text{ }}\infty } \right[\) AG
[5 marks]
(i) rearrange in standard form:
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} + \frac{2}{{x\ln x}}y = \frac{{2x - 1}}{{{{(\ln x)}^2}}},{\text{ }}x > 1\) (A1)
integrating factor:
\({{\text{e}}^{\int {\frac{2}{{x\ln x}}{\text{d}}x} }}\) (M1)
\( = {{\text{e}}^{\ln \left( {{{(\ln x)}^2}} \right)}}\)
\( = {(\ln x)^2}\) (A1)
multiply by integrating factor (M1)
\({(\ln x)^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} + \frac{{2\ln x}}{x}y = 2x - 1\)
\(\frac{{\text{d}}}{{{\text{d}}x}}\left( {y{{(\ln x)}^2}} \right) = 2x - 1{\text{ }}\left( {{\text{or }}y{{(\ln x)}^2} = \int {2x - 1{\text{d}}x} } \right)\) M1
attempt to integrate: M1
\({(\ln x)^2}y = {x^2} - x + c\)
\(y = \frac{{{x^2} - x + c}}{{{{(\ln x)}^2}}}\) A1
(ii) attempt to use the point \(\left( {{\text{e, }}{{\text{e}}^2}} \right)\) to determine c: M1
eg, \({(\ln {\text{e}})^2}{{\text{e}}^2} = {{\text{e}}^2} - {\text{e}} + {\text{c}}\) or \({{\text{e}}^2} = \frac{{{{\text{e}}^2} - {\text{e}} + {\text{c}}}}{{{{(\ln {\text{e}})}^2}}}\) or \({{\text{e}}^2} = {{\text{e}}^2} - {\text{e}} + {\text{c}}\)
\({\text{c}} = {\text{e}}\) A1
\(y = \frac{{{x^2} - x + {\text{e}}}}{{{{(\ln x)}^2}}}\) AG
(iii) 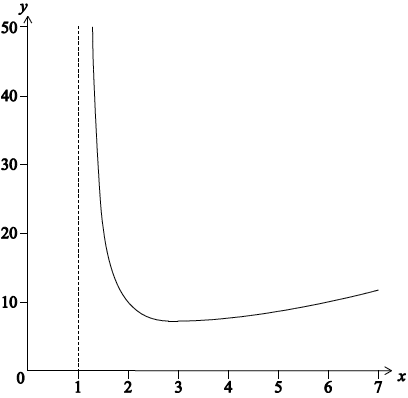
graph with correct shape A1
minimum at \(x = 3.1\) (accept answers to a minimum of 2 s.f) A1
asymptote shown at \(x = 1\) A1
Note: y-coordinate of minimum not required for A1;
Equation of asymptote not required for A1 if VA appears on the sketch.
Award A0 for asymptotes if more than one asymptote are shown
[12 marks]

