| Date | November 2016 | Marks available | 2 | Reference code | 16N.2.hl.TZ0.5 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | State | Question number | 5 | Adapted from | N/A |
Question
Consider the function \(f\) defined by \(f(x) = 3x\arccos (x)\) where \( - 1 \leqslant x \leqslant 1\).
Sketch the graph of \(f\) indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
State the range of \(f\).
Solve the inequality \(\left| {3x\arccos (x)} \right| > 1\).
Markscheme
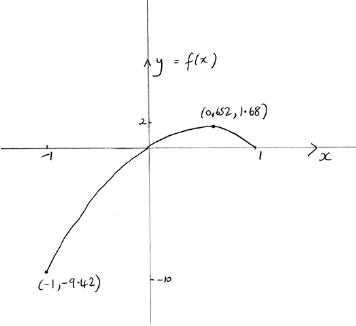
correct shape passing through the origin and correct domain A1
Note: Endpoint coordinates are not required. The domain can be indicated by \( - 1\) and 1 marked on the axis.
\((0.652,{\text{ }}1.68)\) A1
two correct intercepts (coordinates not required) A1
Note: A graph passing through the origin is sufficient for \((0,{\text{ }}0)\).
[3 marks]
\([-9.42,{\text{ }}1.68]{\text{ }}({\text{or }} - 3\pi ,{\text{ }}1.68])\) A1A1
Note: Award A1A0 for open or semi-open intervals with correct endpoints. Award A1A0 for closed intervals with one correct endpoint.
[2 marks]
attempting to solve either \(\left| {3x\arccos (x)} \right| > 1\) (or equivalent) or \(\left| {3x\arccos (x)} \right| = 1\) (or equivalent) (eg. graphically) (M1)
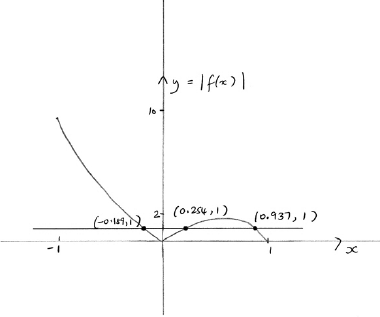
\(x = - 0.189,{\text{ }}0.254,{\text{ }}0.937\) (A1)
\( - 1 \leqslant x < - 0.189{\text{ or }}0.254 < x < 0.937\) A1A1
Note: Award A0 for \(x < - 0.189\).
[4 marks]

