| Date | May 2016 | Marks available | 4 | Reference code | 16M.1.hl.TZ2.3 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
Show that \(\cot \alpha = \tan \left( {\frac{\pi }{2} - \alpha } \right)\) for \(0 < \alpha < \frac{\pi }{2}\).
Hence find \(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x,{\text{ }}0 < \alpha < \frac{\pi }{2}} \).
Markscheme
EITHER
use of a diagram and trig ratios
eg,
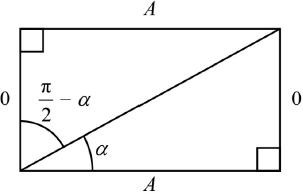
\(\tan \alpha = \frac{O}{A} \Rightarrow \cot \alpha = \frac{A}{O}\)
from diagram, \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \frac{A}{O}\) R1
OR
use of \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }}\) R1
THEN
\(\cot \alpha = \tan \left( {\frac{\pi }{2} - \alpha } \right)\) AG
[1 mark]
\(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x} = [\arctan x]_{\tan \alpha }^{\cot \alpha }\) (A1)
Note: Limits (or absence of such) may be ignored at this stage.
\( = \arctan (\cot \alpha ) - \arctan (\tan \alpha )\) (M1)
\( = \frac{\pi }{2} - \alpha - \alpha \) (A1)
\( = \frac{\pi }{2} - 2\alpha \) A1
[4 marks]
Examiners report
This was generally well done.
This was generally well done. Some weaker candidates tried to solve part (b) through use of a substitution, though the standard result \(\arctan x\) was well known. A small number used \(\arctan x + c\) and went on to obtain an incorrect final answer.

