| Date | November 2014 | Marks available | 2 | Reference code | 14N.3.SL.TZ0.19 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Determine | Question number | 19 | Adapted from | N/A |
Question
This question is about optic fibres.
An optic fibre consists of a thin glass fibre surrounded by a cladding material. The refractive index of the glass is 1.62.
Calculate the critical angle for this optic fibre.
The diagram shows a straight optic fibre. Sketch the passage of a ray of light through the fibre.
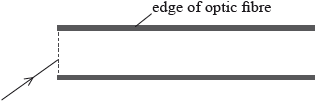
The input power to the fibre is 150 mW. The attenuation per unit length of the glass fibre is \({\text{12.0 dB}}\,{\text{k}}{{\text{m}}^{ - 1}}\). When the light has travelled a distance \(l\) its power has fallen to 3.00 mW, at which point amplification of the signal is required. Determine \(l\).
Markscheme
\(\left( {\sin C = \frac{1}{n} = \frac{1}{{1.62}} \Rightarrow C = } \right){\text{ }}38(.1)^\circ \) or 0.665 rad;
rays with an angle of greater than \({38^ \circ }\) shown with total internal reflection;
normal drawn onto diagram for at least one point;
pairs of angles of incidence and reflection the same;
Judge by eye.
attenuation/\({\text{dB}} = \left( {10\log \frac{{{I_1}}}{{{I_2}}} = } \right){\text{ }}10\log \frac{{3{\text{ mW}}}}{{150{\text{ mW}}}}\)\(\,\,\,\)or\(\,\,\,\)\( - 17.0{\text{ dB}}\);
\({\text{length}} = \left( {\frac{{{\text{attenuation}}}}{{{\text{attenuation per unit length}}}}{\text{ = }}\frac{{ - 17.0}}{{12}} = } \right){\text{ 1.42 km}}\);
Examiners report
(a)(i) was well answered.
In (a)(ii), many candidates were not careful to obey the law of reflection.
Most failed to determine the attenuation in (b).

