| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.SL.TZ0.6 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Determine | Question number | 6 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about kinematics and Newton’s laws of motion.
Part 2 is about electrical circuits.
Part 1 Kinematics and Newton’s laws of motion
Cars I and B are on a straight race track. I is moving at a constant speed of \({\text{45 m}}\,{{\text{s}}^{ - 1}}\) and B is initially at rest. As I passes B, B starts to move with an acceleration of \({\text{3.2 m}}\,{{\text{s}}^{ - 2}}\).
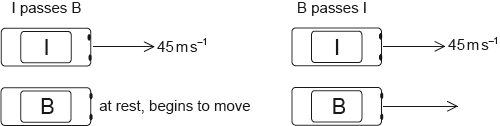
At a later time B passes I. You may assume that both cars are point particles.
A third car O with mass 930 kg joins the race. O collides with I from behind, moving along the same straight line as I. Before the collision the speed of I is \({\text{45 m}}\,{{\text{s}}^{ - 1}}\) and its mass is 850 kg. After the collision, I and O stick together and move in a straight line with an initial combined speed of \({\text{52 m}}\,{{\text{s}}^{ - 1}}\).
This question is in two parts. Part 1 is about kinematics and Newton’s laws of motion.
Part 2 Electrical circuits
The circuit shown is used to investigate how the power developed by a cell varies when the load resistance \(R\) changes.
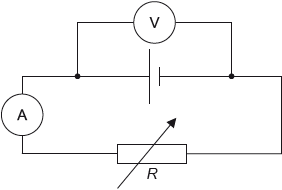
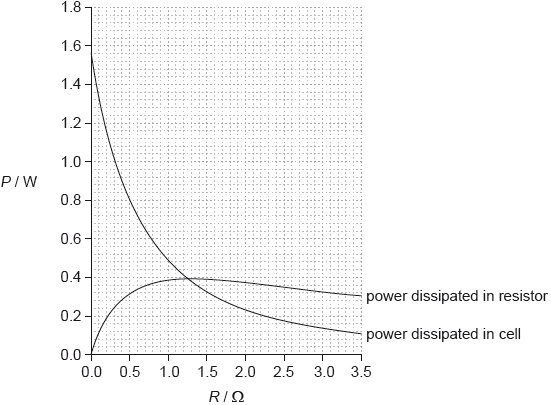
The variable resistor is adjusted and a series of current and voltage readings are taken. The graph shows the variation with \(R\) of the power dissipated in the cell and the power dissipated in the variable resistor.
The cell has an internal resistance.
Show that the time taken for B to pass I is approximately 28 s.
Calculate the distance travelled by B in this time.
B slows down while I remains at a constant speed. The driver in each car wears a seat belt. Using Newton’s laws of motion, explain the difference in the tension in the seat belts of the two cars.
Calculate the speed of O immediately before the collision.
The duration of the collision is 0.45 s. Determine the average force acting on O.
An ammeter and a voltmeter are used to investigate the characteristics of a variable resistor of resistance \(R\). State how the resistance of the ammeter and of the voltmeter compare to \(R\) so that the readings of the instruments are reliable.
Show that the current in the circuit is approximately 0.70 A when \(R = 0.80{\text{ }}\Omega \).
Outline what is meant by the internal resistance of a cell.
Determine the internal resistance of the cell.
Calculate the electromotive force (emf) of the cell.
Markscheme
distances itemized; (it must be clear through use of \({s_I}\) or distance I etc)
distances equated;
\(t = \frac{{2v}}{a}\) / cancel and re-arrange;
substitution \(\left( {\frac{{2 \times 45}}{{3.2}}} \right)\) shown / 28.1(s) seen;
or
clear written statement that the average speed of B must be the same as constant speed of I;
as B starts from rest the final speed must be \({\text{2}} \times {\text{45}}\);
so \(t = \frac{{\Delta v}}{a} = \frac{{90}}{{3.2}}\);
28.1 (s) seen; (for this alternative the method must be clearly described)
or
attempts to compare distance travelled by I and B for 28 s;
I distance \( = (45 \times 28 = ){\text{ }}1260{\text{ (m)}}\);
B distance \( = (\frac{1}{2} \times 3.2 \times {28^2} = ){\text{ }}1255{\text{ (m)}}\);
deduces that overtake must occur about \(\left( {\frac{5}{{45}} = } \right){\text{ }}0.1{\text{ s}}\) later;
use of appropriate equation of motion;
\((1.26 \approx )\) 1.3 (km);
Award [2] for a bald correct answer.
driver I moves at constant speed so no net (extra) force according to Newton 1;
driver B decelerating so (extra) force (to rear of car) (according to Newton 1) / momentum/inertia change so (extra) force must be present;
(hence) greater tension in belt B than belt I;
Award [0] for stating that tension is less in the decelerating car (B).
\(930 \times v + 850 \times 45 = 1780 \times 52\) or statement that momentum is conserved;
\(v = 58{\text{ }}({\text{m}}\,{{\text{s}}^{ - 1}})\);
Allow [2] for a bald correct answer.
use of force \(\frac{{{\text{change of momentum}}}}{{{\text{time}}}}\) (or any variant, eg: \(\frac{{930 \times 6.4}}{{0.45}}\));
\(13.2 \times {10^3}{\text{ (N)}}\); } (must see matched units and value ie: 13 200 without unit gains MP2, 13.2 does not)
Award [2] for a bald correct answer.
Allow use of 58 m s–1 from (c)(i) to give 12 400 (N).
ammeter must have very low resistance/much smaller than \(R\);
voltmeter must have very large resistance/much larger than \(R\);
Allow [1 max] for zero and infinite resistance for ammeter and voltmeter respectively.
Allow [1 max] if superlative (eg: very/much/OWTTE) is missing.
power (loss in resistor) \( = 0.36{\text{ (W)}}\); } (accept answers in the range of 0.35 to 0.37 (W) – treat value outside this range as ECF (could still lead to 0.7))
\({I^2} \times 0.80 = 0.36\);
\(I = 0.67{\text{ (A)}}\) or \(\sqrt {\left( {\frac{{0.36}}{{0.8}}} \right)} \); (allow answers in the range of 0.66 to 0.68 (A).
resistance of the components/chemicals/materials within the cell itself; } (not “resistance of cell”)
leading to energy/power loss in the cell;
power (in cell with 0.7 A) \( = 0.58{\text{ W}}\); } (allow answers in the range of 0.57 W to 0.62 W)
\({0.7^2} \times r = 0.58\);
\(r = 1.2{\text{ (}}\Omega {\text{)}}\); (allow answers in the range of 1.18 to 1.27 (\(\Omega \)))
or
when powers are equal;
\({I^2}R = {I^2}r\);
so \(r = R\) which occurs at 1.2(5) (\(\Omega \));
Award [1 max] for bald 1.2(5) (\(\Omega \)).
\(\left( {E = I(R + r)} \right) = 0.7(0.8 + 1.2)\);
1.4 (V);
Allow ECF from (e) or (f)(ii).
or
when \(R = 0\), power loss \( = 1.55\);
\(E = (\sqrt {1.55 \times 1.2} = ){\text{ }}1.4{\text{ (V)}}\);

