| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.HL.TZ0.6 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Draw | Question number | 6 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about electric fields and radioactive decay. Part 2 is about waves.
Part 1 Electric fields and radioactive decay
An ionization chamber is a device which can be used to detect charged particles.
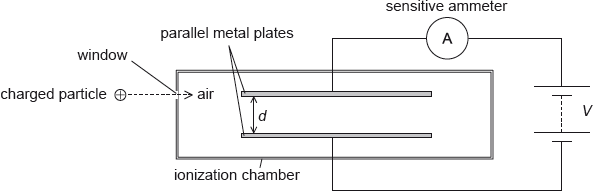
The charged particles enter the chamber through a thin window. They then ionize the air between the parallel metal plates. A high potential difference across the plates creates an electric field that causes the ions to move towards the plates. Charge now flows around the circuit and a current is detected by the sensitive ammeter.
The separation of the plates d is 12 mm and the potential difference \(V\) between the plates is 5.2 kV. An ionized air molecule M with charge \( + 2e\) is produced when a charged particle collides with an air molecule.
Radium-226 \({\text{(}}_{\;{\text{88}}}^{{\text{226}}}{\text{Ra)}}\) decays into an isotope of radon (Rn) by the emission of an alpha particle and a gamma-ray photon. The alpha particle may be detected using the ionization chamber but the gamma-ray photon is unlikely to be detected.
On the diagram, draw the shape of the electric field between the plates.
Calculate the electric field strength between the plates.
Calculate the force on M.
Determine the change in the electric potential energy of M as it moves from the positive to the negative plate.
Construct the nuclear equation for the decay of radium-226.
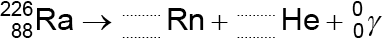
Radium-226 has a half-life of 1600 years. Determine the time, in years, it takes for the activity of radium-226 to fall to 5% of its original activity.
Markscheme
minimum of three lines equally spaced and distributed, perpendicular to the plates and downwards; edge effect shown; } (condone lines that do not touch plates)
\(4.3 \times {10^5}{\text{ (N}}{{\text{C}}^{ - 1}}{\text{)}}\)
\((F = Eq = ){\text{ }}4.3 \times {10^5} \times 2 \times 1.6 \times {10^{ - 19}}\); (allow ECF from (b)(i))
\(1.4 \times {10^{ - 13}}{\text{ (N)}}\);
Award [2] for a bald correct answer.
\(\Delta {E_{\text{P}}} = q\Delta V\)\(\,\,\,\)or\(\,\,\,\)\(3.2 \times {10^{ - 19}} \times 5.2 \times {10^3}\);
\(1.7 \times {10^{ - 15}}{\text{ (J)}}\);
negative/loss;
\(\left( {_{\;88}^{226}{\text{Ra}} \to _{\;86}^{222}{\text{Rn}} + _2^4{\text{He}} + _0^0\gamma } \right)\)
\(_{\;86}^{222}{\text{Rn}}\)\(\,\,\,\)or\(\,\,\,\)\(_2^4{\text{He}}\);
numbers balance top and bottom on right-hand side;
\(\lambda = \frac{{\ln 2}}{{1600}} = 4.33 \times {10^{ - 4}}{\text{ (y}}{{\text{r}}^{ - 1}}{\text{)}}\);
\(0.05 = {{\text{e}}^{ - \lambda t}}\);
6900 (years);
Award [3] for a bald correct answer.
Award [2 max] for 2.18 \( \times \) 1011 (s).
Award [1 max] to a candidate who identifies time as about 4.3 half-lives but cannot get further or gives an approximate reasoned answer.
However award [3] if number n of half-lives is calculated from 0.05 = 2–n (= 4.32 usually from use of log2 working) and time shown.
Examiners report
Field patterns were often negligently drawn. Lines did not meet both plates, edge effects were ignored, and the (vital) equality of spacing between drawn lines was not considered. Candidates continue to show their inadequacy in responding to questions that demand a careful and accurate diagram.
This sequence of calculations was often undertaken well with appropriate figures carried through from part to part.
This sequence of calculations was often undertaken well with appropriate figures carried through from part to part.
This sequence of calculations was often undertaken well with appropriate figures carried through from part to part. The only common error was the omission of a consideration of the gain or loss of the energy change in part (iii).
As one of the easiest questions on the paper this was predictably well done.
In the past candidates have found calculation involving exponential change difficult. On this occasion, however examiners saw a large number of correct and well explained solutions from candidates.

