| Date | May 2018 | Marks available | 3 | Reference code | 18M.2.HL.TZ2.8 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 8 | Adapted from | N/A |
Question
A negatively charged thundercloud above the Earth’s surface may be modelled by a parallel plate capacitor.
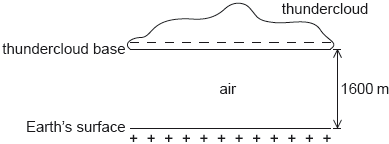
The lower plate of the capacitor is the Earth’s surface and the upper plate is the base of the thundercloud.
The following data are available.
\[\begin{array}{*{20}{l}} {{\text{Area of thundercloud base}}}&{ = 1.2 \times {{10}^8}{\text{ }}{{\text{m}}^2}} \\ {{\text{Charge on thundercloud base}}}&{ = -25{\text{ C}}} \\ {{\text{Distance of thundercloud base from Earth's surface}}}&{ = 1600{\text{ m}}} \\ {{\text{Permittivity of air}}}&{ = 8.8 \times {{10}^{ - 12}}{\text{ F }}{{\text{m}}^{ - 1}}} \end{array}\]
Lightning takes place when the capacitor discharges through the air between the thundercloud and the Earth’s surface. The time constant of the system is 32 ms. A lightning strike lasts for 18 ms.
Show that the capacitance of this arrangement is C = 6.6 × 10–7 F.
Calculate in V, the potential difference between the thundercloud and the Earth’s surface.
Calculate in J, the energy stored in the system.
Show that about –11 C of charge is delivered to the Earth’s surface.
Calculate, in A, the average current during the discharge.
State one assumption that needs to be made so that the Earth-thundercloud system may be modelled by a parallel plate capacitor.
Markscheme
C = «ε\(\frac{A}{d}\) =» 8.8 × 10–12 × \(\frac{{1.2 \times {{10}^8}}}{{1600}}\)
«C = 6.60 × 10–7 F»
[1 mark]
V = «\(\frac{Q}{C}\) =» \(\frac{{25}}{{6.6 \times {{10}^{ - 7}}}}\)
V = 3.8 × 107 «V»
Award [2] for a bald correct answer
[2 marks]
ALTERNATIVE 1
E = «\(\frac{1}{2}\)QV =» \(\frac{1}{2}\) × 25 × 3.8 × 107
E = 4.7 × 108 «J»
ALTERNATIVE 2
E = «\(\frac{1}{2}\)CV2 =» \(\frac{1}{2}\) × 6.60 × 10–7 × (3.8 × 107)2
E = 4.7 × 108 «J» / 4.8 × 108 «J» if rounded value of V used
Award [2] for a bald correct answer
Allow ECF from (b)(i)
[2 marks]
Q = «\({Q_0}{e^{ - \frac{t}{\tau }}}\) =» 25 × \({e^{ - \frac{{18}}{{32}}}}\)
Q = 14.2 «C»
charge delivered = Q = 25 – 14.2 = 10.8 «C»
«≈ –11 C»
Final answer must be given to at least 3 significant figures
[3 marks]
I «= \(\frac{{\Delta Q}}{{\Delta t}} = \frac{{11}}{{18 \times {{10}^{ - 3}}}}\)» ≈ 610 «A»
Accept an answer in the range 597 − 611 «A»
[1 mark]
the base of the thundercloud must be parallel to the Earth surface
OR
the base of the thundercloud must be flat
OR
the base of the cloud must be very long «compared with the distance from the surface»
[1 mark]

