| Date | November 2010 | Marks available | 3 | Reference code | 10N.3.SL.TZ0.A2 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Outline | Question number | A2 | Adapted from | N/A |
Question
This question is about diffraction and resolution.
A parallel beam of monochromatic light is incident on a narrow rectangular slit. After passing through the slit, the light is incident on a distant screen.
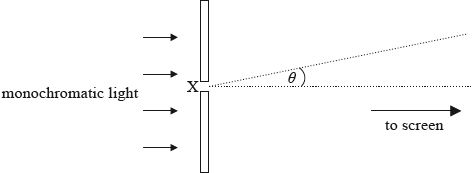
Point X is the midpoint of the slit.
(i) On the axes below, sketch a graph to show how the intensity of the light on the screen varies with the angle \(\theta \) shown in the diagram.
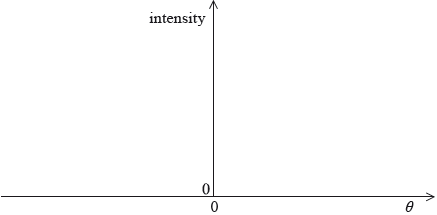
(ii) The wavelength of the light is 520 nm, the width of the slit is 0.04 mm and the screen is 1.2 m from the slit. Show that the width of the central maximum of intensity on the screen is about 3 cm.
Points P and Q are on the circumference of a planet as shown.
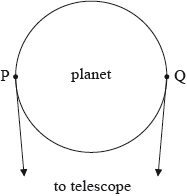
By considering the two points, outline why diffraction limits the ability of an astronomical telescope to resolve the image of the planet as a disc.
Markscheme
(i) 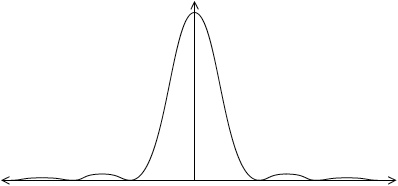
general correct shape touching axis and symmetric about \(\theta = 0\) (at least onesecondary maxima on each side); (judge by eye)
central maximum wider than secondary maxima;
secondary maxima at most one third intensity of central maximum;
(ii) \(\frac{d}{2} = \frac{{D\lambda }}{b}\);
\(d = \frac{{2.0 \times 1.2 \times 5.2 \times {{10}^{ - 7}}}}{{4.0 \times {{10}^{ - 5}}}} = 3.12 \times {10^{ - 2}}{\text{ m}}\);
\( \approx 3{\text{ cm}}\)
Award [2 max] for a sensible argument.
e.g. light from each point forms a diffraction pattern after being focussed by the eyepiece of the telescope;
if the diffraction patterns are not sufficiently well separated then the points will not be resolved as separate sources;
Award [1 max] for the conclusion.
e.g. if the points cannot be resolved as separate sources the planet cannot be seen as a disc;
Examiners report
Intensity distributions were often drawn well but quite a few candidates did not have their graphs in contact with the \(\theta \) axis. Candidates’ working was often difficult to follow in the calculation part of this question.
Very few candidates recognised the role played by diffraction in the resolution of the planet as a disc.

