| Date | November 2010 | Marks available | 3 | Reference code | 10N.2.SL.TZ0.B3 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Discuss | Question number | B3 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the production of energy in nuclear fission. Part 2 is about collisions.
Part 1 Production of energy in nuclear fission
A possible fission reaction is
\[_{\;92}^{235}U + _0^1n \to _{36}^{92}Kr + _{\;56}^{141}Ba + x_0^1n.\]
Part 2 Collisions
In an experiment, an air-rifle pellet is fired into a block of modelling clay that rests on a table.
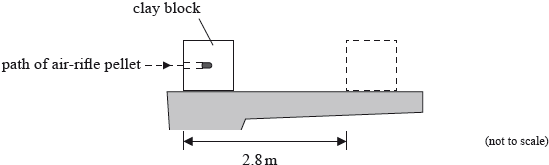
The air-rifle pellet remains inside the clay block after the impact.
As a result of the collision, the clay block slides along the table in a straight line and comes to rest. Further data relating to the experiment are given below.
\[\begin{array}{*{20}{l}} {{\text{Mass of air - rifle pellet}}}&{ = 2.0{\text{ g}}} \\ {{\text{Mass of clay block}}}&{ = 56{\text{ g}}} \\ {{\text{Velocity of impact of air - rifle pellet}}}&{ = 140{\text{ m}}\,{{\text{s}}^{ - 1}}} \\ {{\text{Stopping distance of clay block}}}&{ = 2.8{\text{ m}}} \end{array}\]
(i) State the value of \(x\).
(ii) Show that the energy released when one uranium nucleus undergoes fission in the reaction in (a) is about \(2.8 \times {10^{ - 11}}{\text{ J}}\).
\[\begin{array}{*{20}{l}} {{\text{Mass of neutron}}}&{ = 1.00867{\text{ u}}} \\ {{\text{Mass of U - 235 nucleus}}}&{ = 234.99333{\text{ u}}} \\ {{\text{Mass of Kr - 92 nucleus}}}&{ = 91.90645{\text{ u}}} \\ {{\text{Mass of Ba - 141 nucleus}}}&{ = 140.88354{\text{ u}}} \end{array}\]
(iii) State how the energy of the neutrons produced in the reaction in (a) is likely to compare with the energy of the neutron that initiated the reaction.
Outline the role of the moderator.
A nuclear power plant that uses U-235 as fuel has a useful power output of 16 MW and an efficiency of 40%. Assuming that each fission of U-235 gives rise to \(2.8 \times {10^{ - 11}}{\text{ J}}\) of energy, determine the mass of U-235 fuel used per day.
State the principle of conservation of momentum.
(i) Show that the initial speed of the clay block after the air-rifle pellet strikes it is \(4.8{\text{ m}}\,{{\text{s}}^{ - 1}}\).
(ii) Calculate the average frictional force that the surface of the table exerts on the clay block whilst the clay block is moving.
Discuss the energy transformations that occur in the clay block and the air-rifle pellet from the moment the air-rifle pellet strikes the block until the clay block comes to rest.
The clay block is dropped from rest from the edge of the table and falls vertically to the ground. The table is 0.85 m above the ground. Calculate the speed with which the clay block strikes the ground.
Markscheme
(i) 3;
(ii) \(\Delta m = 234.99333 - 91.90645 - 140.88354 - [2 \times 1.00867]\);
\( = 0.186{\text{ (u)}}\);
\({\text{energy released}} = 0.186 \times 931 = 173{\text{ }}({\text{MeV)}}\);
\(173 \times {10^6} \times 1.6 \times {10^{ - 19}}\);
\(( = 2.768) \approx 2.8 \times {10^{ - 11}}{\text{ (J)}}\)
or
\(\Delta m = 234.99333 - 91.90645 - 140.88354 - [2 \times 1.00867]\);
\( = 0.186{\text{ (u)}}\);
\({\text{mass converted}} = 0.186 \times 1.66 \times {10^{ - 27}}{\text{ }}( = 3.09 \times {10^{ - 28}})\);
(use of \(E = m{c^2}\)) \({\text{energy}} = 3.09 \times {10^{ - 28}} \times 9 \times {10^{ - 16}}\);
\(( = 2.77) \approx 2.8 \times {10^{ - 11}}{\text{ (J)}}\)
Award [2 max] if mass difference is incorrect.
If candidate carries forward an incorrect value from (a)(i) [2 is common], treat this as ecf in (a)(ii).
Award [3 max] if the candidate uses a value for x inconsistent with (a)(i).
(iii) greater/higher energy;
reduces neutron speed to (thermal) lower speeds;
so that chance of initiating fission is higher;
Accept “fast neutrons cannot cause fission” for 2nd marking point.
40% efficient so 40 (MW) required;
\(\frac{{40 \times {{10}^6}}}{{2.8 \times {{10}^{ - 11}}}} = 1.43 \times {10^{18}}\) per second;
number of fissions per day \( = 1.23 \times {10^{23}}\);
\(\left( { = \frac{{1.23 \times {{10}^{23}} \times 235}}{{6 \times {{10}^{23}}}}} \right) = {\text{48 g per day}}\);
the total momentum of a system is constant;
provided external force does not act;
or
the momentum of an isolated/closed system;
is constant;
Award [1] for momentum before collision equals collision afterwards.
(i) initial momentum \( = 2.0 \times {10^{ - 3}} \times 140\);
final speed \(\frac{{2.0 \times {{10}^{ - 3}} \times 140}}{{5.6 \times {{10}^{ - 2}} + 2.0 \times {{10}^{ - 3}}}}\);
\( = 4.8{\text{ m}}\,{{\text{s}}^{ - 1}}\)
Watch for incorrect mass values in equation.
(ii) initial kinetic energy of pellet \( + \) clay block \( = \frac{1}{2}m{v^2}\);
\(0.5 \times 0.058 \times {4.8^2}{\text{ (}} = 0.67{\text{ J)}}\);
\({\text{force}} = \frac{{{\text{work done}}}}{{{\text{distance travelled}}}}\);
\( = 0.24{\text{ N}}\);
or
use of appropriate kinematic equation with consistent sign usage e.g. \(a = \frac{{{u^2} - {v^2}}}{{2s}}\);
\(a = \frac{{{{4.8}^2}}}{{2 \times 2.8}}\);
\(F = \frac{{0.058 \times {{4.8}^2}}}{{2 \times 2.8}}\);
\( = 0.24{\text{ N}}\);
kinetic energy of pellet is transferred to kinetic energy of clay block;
and internal energy of pellet and clay block;
clay block loses kinetic energy as thermal energy/heat;
\(v = \sqrt {2gs} \);
\( = 4.1{\text{ m}}\,{{\text{s}}^{ - 1}}\);
Allow g \( = \) 10 m\(\,\)s–2 answer 4.1 m\(\,\)s–2
Award [2] for bald correct answer.
Examiners report
(i) A common incorrect answer was 2.
(ii) Candidates were often able to carry this calculation through to a correct conclusion. It was a “show that” and a high level of explanation was required by examiners and was – in many cases – demonstrated.
(iii) Reponses here were mostly correct. However, the answer “It has a higher energy” was common. Candidates need to be reminded of the imprecision of such a statement. Is “It” the initiating neutron or the emitted neutron?
Weaker candidates could not distinguish between the role of the moderator and that of the control rods.
Many good calculations were seen but weaker candidates usually arrived at recognition that the required power from the reactor is 40 MW and could go no further.
When the question is “State the principle of conservation of momentum.” an answer of “momentum is conserved” will attract no marks. The examiner needs to know what “conserved” means. Many omitted the statement that external forces do not act (or similar)
(i) Careful examination of solutions showed that about one-third of candidate forgot to add the mass of the pellet to the final total mass of the block.
(ii) This two-stage calculation attracted the same error as part (i) and many power of ten errors through a failure to note the units of mass in the question.
Descriptions of the energy transformations were incomplete and poorly described. There was a general failure to recognise that the pellet transfers its kinetic energy into a number of distinct forms. Candidates are too quick to ascribe energy loss to “friction” without indicating the seat of this energy loss.
Most candidates were able to complete this calculation or to get close to it. Some forgot to evaluate the square root having arrived at the speed squared.

