| Date | None Specimen | Marks available | 3 | Reference code | SPNone.2.hl.TZ0.4 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Copy and complete | Question number | 4 | Adapted from | N/A |
Question
The binary operation multiplication modulo \(9\), denoted by \({ \times _9}\) , is defined on the set \(S = \left\{ {1,2,3,4,5,6,7,8} \right\}\) .
Copy and complete the following Cayley table.
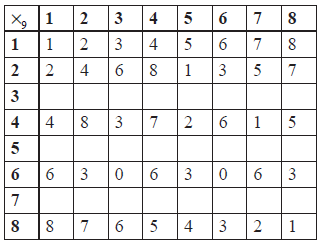
Show that \(\left\{ {S,{ \times _9}} \right\}\) is not a group.
Prove that a group \(\left\{ {G,{ \times _9}} \right\}\) can be formed by removing two elements from the set \(S\) .
(i) Find the order of all the elements of \(G\) .
(ii) Write down all the proper subgroups of \(\left\{ {G,{ \times _9}} \right\}\) .
(iii) Determine the coset containing the element \(5\) for each of the subgroups in part (ii).
Solve the equation \(4{ \times _9}x{ \times _9}x = 1\) .
Markscheme
A3
Note: Award A2 if one error, A1 if two errors and A0 if three or more errors.
[3 marks]
any valid reason, R1
e.g. not closed
\(3\) or \(6\) has no inverse,
it is not a Latin square
[1 mark]
remove \(3\) and \(6\) A1
for the remaining elements,
the table is closed R1
associative because multiplication is associative R1
the identity is \(1\) A1
every element has an inverse, (\(2\), \(5\)) and (\(4\), \(7\)) are inverse pairs and \(8\) (and \(1\)) are self-inverse A1
thus it is a group AG
[5 marks]
(i) the orders are
A3
Note: Award A2 if one error, A1 if two errors and A0 if three or more errors.
(ii) the proper subgroups are
\(\left\{ {1,8} \right\}\) A1
\(\left\{ {1,4,7} \right\}\) A1
Note: Do not penalize inclusion of \(\left\{ 1 \right\}\) .
(iii) the cosets are \(\left\{ {5,4} \right\}\) (M1)A1
\(\left\{ {5,2,8} \right\}\) A1
[8 marks]
\(x{ \times _9}x = 7\) (A1)
\(x = 4,5\) A1A1
[3 marks]

