| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.hl.TZ0.3 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Construct | Question number | 3 | Adapted from | N/A |
Question
Consider the set \(S = \{ 0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5\} \) under the operation of addition modulo \(6\), denoted by \({ + _6}\).
Construct the Cayley table for \(\{ S,{\text{ }}{ + _6}\} \).
Show that \(\{ S,{\text{ }}{ + _6}\} \) forms an Abelian group.
State the order of each element.
Explain whether or not the group is cyclic.
Markscheme
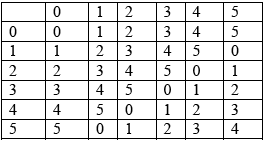 A2
A2
Note: A1 for one or two errors in the table, A0 otherwise.
closed no new elements A1
\(0\) is identity (since \(0 + a = a + 0 = a,{\text{ }}a \in S\)) A1
\(0\), \(3\) self inverse, \(1 \Leftrightarrow 5\) inverse pair, \(2 \Leftrightarrow 4\) inverse pair A1
all elements have an inverse
associativity is assumed over addition A1
since symmetry on leading diagonal in table or commutativity of addition A1
\( \Rightarrow \{ S,{\text{ }}{ + _6}\} \) is an Abelian group AG
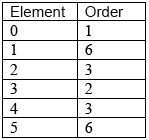 A2
A2
Note: A1 for one or two errors in the table, A0 otherwise.
since there is an element with order \(6\) OR \(1\) or \(5\) are generators R1
the group is cyclic A1
Examiners report
This question was well answered in general although some candidates showed only commutativity, not realising that they also had to prove that it was a group.
This question was well answered in general although some candidates showed only commutativity, not realising that they also had to prove that it was a group.
This question was well answered in general although some candidates showed only commutativity, not realising that they also had to prove that it was a group.
This question was well answered in general although some candidates showed only commutativity, not realising that they also had to prove that it was a group.

