| Date | May 2012 | Marks available | 3 | Reference code | 12M.2.hl.TZ0.4 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 4 | Adapted from | N/A |
Question
The function \(f:\mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) is defined by \(\boldsymbol{X} \mapsto \boldsymbol{AX}\) , where \(\boldsymbol{X} = \left[ \begin{array}{l}
x\\
y
\end{array} \right]\) and \(\boldsymbol{A} = \left[ \begin{array}{l}
a\\
c
\end{array} \right.\left. \begin{array}{l}
b\\
d
\end{array} \right]\) where \(a\) , \(b\) , \(c\) , \(d\) are all non-zero.
Consider the group \(\left\{ {S,{ + _m}} \right\}\) where \(S = \left\{ {0,1,2 \ldots m - 1} \right\}\) , \(m \in \mathbb{N}\) , \(m \ge 3\) and \({ + _m}\) denotes addition modulo \(m\) .
Show that \(f\) is a bijection if \(\boldsymbol{A}\) is non-singular.
Suppose now that \(\boldsymbol{A}\) is singular.
(i) Write down the relationship between \(a\) , \(b\) , \(c\) , \(d\) .
(ii) Deduce that the second row of \(\boldsymbol{A}\) is a multiple of the first row of \(\boldsymbol{A}\) .
(iii) Hence show that \(f\) is not a bijection.
Show that \(\left\{ {S,{ + _m}} \right\}\) is cyclic for all m .
Given that \(m\) is prime,
(i) explain why all elements except the identity are generators of \(\left\{ {S,{ + _m}} \right\}\) ;
(ii) find the inverse of \(x\) , where x is any element of \(\left\{ {S,{ + _m}} \right\}\) apart from the identity;
(iii) determine the number of sets of two distinct elements where each element is the inverse of the other.
Suppose now that \(m = ab\) where \(a\) , \(b\) are unequal prime numbers. Show that \(\left\{ {S,{ + _m}} \right\}\) has two proper subgroups and identify them.
Markscheme
recognizing that the function needs to be injective and surjective R1
Note: Award R1 if this is seen anywhere in the solution.
injective:
let \(\boldsymbol{U}, \boldsymbol{V} \in ^\circ \times ^\circ \) be 2-D column vectors such that \(\boldsymbol{AU} = \boldsymbol{AV}\) M1
\({\boldsymbol{A}^{ - 1}}\boldsymbol{AU} = {\boldsymbol{A}^{ - 1}}\boldsymbol{AV}\) M1
\(\boldsymbol{U} = \boldsymbol{V}\) A1
this shows that \(f\) is injective
surjective:
let \(W \in ^\circ \times ^\circ \) M1
then there exists \(\boldsymbol{Z} = {\boldsymbol{A}^{ - 1}}\boldsymbol{W} \in ^\circ \times ^\circ \) such that \(\boldsymbol{AZ} = \boldsymbol{W}\) M1A1
this shows that \(f\) is surjective
therefore \(f\) is a bijection AG
[7 marks]
(i) the relationship is \(ad = bc\) A1
(ii) it follows that \(\frac{c}{a} = \frac{d}{b} = \lambda \) so that \((c,d) = \lambda (a,b)\) A1
(iii) EITHER
let \(\boldsymbol{W} = \left[ \begin{array}{l}
p\\
q
\end{array} \right]\) be a 2-D vector
then \(\boldsymbol{AW} = \left[ \begin{array}{l}
a\\
\lambda a
\end{array} \right.\left. \begin{array}{l}
b\\
\lambda b
\end{array} \right]\left[ \begin{array}{l}
p\\
q
\end{array} \right]\) M1
\( = \left[ \begin{array}{l}
ap + bq\\
\lambda (ap + bq)
\end{array} \right]\) A1
the image always satisfies \(y = \lambda x\) so \(f\) is not surjective and therefore not a bijection R1
OR
consider
\(\left[ {\begin{array}{*{20}{c}}
a&b \\
{\lambda a}&{\lambda b}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
b \\
0
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{ab} \\
{\lambda ab}
\end{array}} \right]\)
\(\left[ {\begin{array}{*{20}{c}}
a&b \\
{\lambda a}&{\lambda b}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
0 \\
a
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{ab} \\
{\lambda ab}
\end{array}} \right]\)
this shows that \(f\) is not injective and therefore not a bijection R1
[5 marks]
the identity element is \(0\) R1
consider, for \(1 \le r \le m\) ,
using \(1\) as a generator M1
\(1\) combined with itself \(r\) times gives \(r\) and as \(r\) increases from \(1\) to m, the group is generated ending with \(0\) when \(r = m\) A1
it is therefore cyclic AG
[3 marks]
(i) by Lagrange the order of each element must be a factor of \(m\) and if \(m\) is prime, its only factors are \(1\) and \(m\) R1
since 0 is the only element of order \(1\), all other elements are of order \(m\) and are therefore generators R1
(ii) since \(x{ + _m}(m - x) = 0\) (M1)
the inverse of x is \((m - x)\) A1
(iii) consider
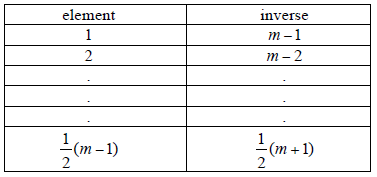 M1A1
M1A1
there are \(\frac{1}{2}(m - 1)\) inverse pairs A1 N1
Note: Award M1 for an attempt to list the inverse pairs, A1 for completing it correctly and A1 for the final answer.
[7 marks]
since \(a\), \(b\) are unequal primes the only factors of \(m\) are \(a\) and \(b\)
there are therefore only subgroups of order \(a\) and \(b\) R1
they are
\(\left\{ {0,a,2a, \ldots ,(b - 1)a} \right\}\) A1
\(\left\{ {0,b,2b, \ldots ,(a - 1)b} \right\}\) A1
[3 marks]
Examiners report
This proved to be a difficult question for some candidates. Most candidates realised that they had to show that the function was both injective and surjective but many failed to give convincing proofs. Some candidates stated, incorrectly, that f was injective because \(\boldsymbol{AX}\) is uniquely defined, not realising that they had to show that \(\boldsymbol{AX} = \boldsymbol{AY} \Rightarrow \boldsymbol{X} = \boldsymbol{Y}\) .
Solutions to (b) were disappointing with many candidates failing to realise that they had either to show that \(\boldsymbol{AX}\) was confined to a subset of \(\mathbb{R} \times \mathbb{R}\) or that two distinct vectors had the same image under \(f\).
This question was well answered in general with solutions to (c) being the least successful.
This question was well answered in general with solutions to (c) being the least successful.
This question was well answered in general with solutions to (c) being the least successful.

