| Date | May 2010 | Marks available | 17 | Reference code | 10M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Determine, Show that, Solve, and Copy and complete | Question number | 1 | Adapted from | N/A |
Question
The binary operator \( * \) is defined for a , \(b \in \mathbb{R}\) by \(a * b = a + b - ab\) .
(i) Show that \( * \) is associative.
(ii) Find the identity element.
(iii) Find the inverse of \(a \in \mathbb{R}\) , showing that the inverse exists for all values of \(a\) except one value which should be identified.
(iv) Solve the equation \(x * x = 1\) .
The domain of \( * \) is now reduced to \(S = \left\{ {0,2,3,4,5,\left. 6 \right\}} \right.\) and the arithmetic is carried out modulo \(7\).
(i) Copy and complete the following Cayley table for \(\left\{ {S,\left. * \right\}} \right.\) .
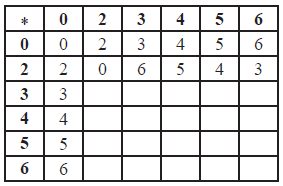
(ii) Show that \(\left\{ {S,\left. * \right\}} \right.\) is a group.
(iii) Determine the order of each element in S and state, with a reason, whether or not \(\left\{ {S,\left. * \right\}} \right.\) is cyclic.
(iv) Determine all the proper subgroups of \(\left\{ {S,\left. * \right\}} \right.\) and explain how your results illustrate Lagrange’s theorem.
(v) Solve the equation \(2 * x * x = 5\) .
Markscheme
(i) \(a * (b * c) = a * (b + c - bc)\) M1
\( = a + b + c - bc - a(b + c - bc)\) A1
\( = a + b + c - bc - ca - ab + abc\) A1
\((a * b) * c = (a + b - ab) * c\) M1
\( = a + b - ab + c - (a + b - ab)c\) A1
\( = a + b + c - bc - ca - ab + abc\) , hence associative AG
(ii) let \(e\) be the identity element, so that \(a * e = a\) (M1)
then,
\(a + e - ae = a\) A1
\(e(1 - a) = 0\)
\(e = 0\) A1
(iii) let \({a^{ - 1}}\) be the inverse of \(a\), so that \(a * {a^{ - 1}} = 0\) (M1)
then,
\(a + {a^{ - 1}} - a{a^{ - 1}} = 0\) A1
\({a^{ - 1}} = \frac{a}{{a - 1}}\) A1
this gives an inverse for all elements except 1 which has no inverse R1
(iv) \(2x - {x^2} = 1\) M1
\({(x - 1)^2} = 0\) (A1)
\(x = 1\) A1
[15 marks]
(i)
 A3
A3
Note: Award A3 for correct table, A2 for one error, A1 for two errors and A0 for more than two errors.
(ii) there are no new elements in the table so it is closed A1
there is an identity element, \(0\) A1
every row (column) has a \(0\) so every element has an inverse A1
associativity has been proved earlier A1
therefore \(\left\{ {S,\left. * \right\}} \right.\) is a group AG
(iii)
 A3
A3
Note: Award A3 for correct table, A2 for one error, A1 for two errors and A0 for more than two errors.
it is cyclic because there are elements of order \(6\) R1
(iv) the proper subgroups are \(\left\{ {0,\left. 2 \right\}} \right.\) , \(\left\{ {0,\left. {4,6} \right\}} \right.\) A1A1
the orders of the subgroups (\(2\), \(3\)) are factors of the order of the group (6) A1
(v) recognizing \(x * x = 4\) (M1)
\(x = 3\) , \(6\) A1A1
[17 marks]
Examiners report
This question was well answered by many candidates. The most common error in (a) was confusing associativity with commutativity.
Many wholly correct or almost wholly correct answers to part (b) were seen. Those who did make errors in part (b) were usually unable to fully justify the properties of a group, could not explain why the group was cyclic or could not relate subgroups to Lagrange’s theorem. Some candidates made errors in calculating the orders of the elements.

