| Date | May 2009 | Marks available | 3 | Reference code | 09M.2.hl.TZ0.2 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 2 | Adapted from | N/A |
Question
A group has exactly three elements, the identity element \(e\) , \(h\) and \(k\) . Given the operation is denoted by \( \otimes \) , show that
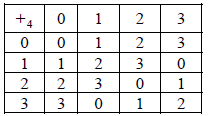
(i) Show that \({\mathbb{Z}_4}\) (the set of integers modulo 4) together with the operation \({ + _4}\) (addition modulo 4) form a group \(G\) . You may assume associativity.
(ii) Show that \(G\) is cyclic.
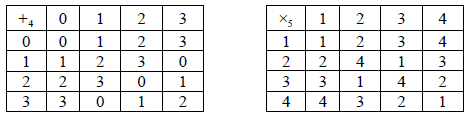
Using Cayley tables or otherwise, show that \(G\) and \(H = \left( {\left\{ {1,2,3,\left. 4 \right\},{ \times _5}} \right.} \right)\) are isomorphic where \({{ \times _5}}\) is multiplication modulo 5. State clearly all the possible bijections.
the group is cyclic.
the group is cyclic.
Markscheme
(i)
 A2
A2
Note: Award A1 for table if exactly one error and A0 if more than one error.
all elements belong to \({\mathbb{Z}_4}\) so it is closed A1
\(0\) is the identity element A1
\(2\) is self inverse A1
\(1\) and \(3\) are an inverse pair A1
hence every element has an inverse
hence \(\left\{ {{\mathbb{Z}_4},{ + _4}} \right\}\) form a group \(G\) AG
(ii) \(1{ + _4}1 \equiv 2(\bmod 4)\)
\(1{ + _4}1{ + _4}1 \equiv 3(\bmod 4)\)
\(1{ + _4}1{ + _4}1{ + _4}1 \equiv 0(\bmod 4)\) M1A1
hence \(1\) is a generator R1
therefore \(G\) is cyclic AG
(\(3\) is also a generator)
[9 marks]
 A1A1
A1A1
EITHER
for the group \(\left( {\left\{ {1,2,3,\left. 4 \right\},{ \times _5}} \right.} \right)\)
\(1\) is the identity and \(4\) is self inverse A1
\(2\) and \(3\) are an inverse pair A1
OR
for \(G\), for \(H\),
0 has order 1 1 has order 1
1 has order 4 2 has order 4
2 has order 2 3 has order 4
3 has order 4 4 has order 2 A1A1
THEN
hence there is a bijection R1
\(h(1) \to 0\) , \(h(2) \to 1\) , \(h(3) \to 3\) , \(h(4) \to 2\) A1
the groups are isomorphic AG
\(k(1) \to 0\) , \(k(2) \to 3\) , \(k(3) \to 1\) , \(k(4) \to 2\) A1
is also a bijection
[7 marks]
if cyclic then the group is {\(e\), \(h\), \({h^2}\)} R1
\({h^2} = e\) or \(h\) or \(k\) M1
\({h^2} = e \Rightarrow h \otimes h = h \otimes k\)
\( \Rightarrow h = k\)
but \(h \ne k\) so \({h^2} \ne e\) A1
\({h^2} = h \Rightarrow h \otimes h = h \otimes e \Rightarrow h = e\)
but \(h \ne e\) so \({h^2} \ne h\)
so \({h^2} = k\) A1
also \({h^3} = h \otimes k = e\)
hence the group is cyclic AG
Note: An alternative proof is possible based on order of elements and Lagrange.
[5 marks]
if cyclic then the group is \(\left\{ {e,h,\left. {{h^2}} \right\}} \right.\) R1
\({h^2} = e\) or \(h\) or \(k\) M1
\({h^2} = e \Rightarrow h \otimes h = h \otimes k\)
\( \Rightarrow h = k\)
but \(h \ne k\) so \({h^2} \ne e\) A1
\({h^2} = h \Rightarrow h \otimes h = h \otimes e \Rightarrow h = e\)
but \(h \ne e\) so \({h^2} \ne h\)
so \({h^2} = k\) A1
also \({h^3} = h \otimes k = e\) A1
hence the group is cyclic AG
Note: An alternative proof is possible based on order of elements and Lagrange.
[5 marks]
Examiners report
Most candidates drew a table for this part and generally achieved success in both (i) and (ii).
In (b) most did use Cayley tables and managed to match element order but could not clearly state the two possible bijections. Sometimes showing that the two groups were isomorphic was missed.
Part B was not well done and the properties of a three element group were often quoted without any proof.
Part B was not well done and the properties of a three element group were often quoted without any proof.

