| Date | May 2015 | Marks available | 5 | Reference code | 15M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find and Hence | Question number | 1 | Adapted from | N/A |
Question
Consider the differential equation \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2x + y - 1\) with boundary condition \(y = 1\) when \(x = 0\).
Using Euler’s method with increments of \(0.2\), find an approximate value for \(y\) when \(x = 1\).
Explain how Euler’s method could be improved to provide a better approximation.
Solve the differential equation to find an exact value for \(y\) when \(x = 1\).
(i) Find the first three non-zero terms of the Maclaurin series for \(y\).
(ii) Hence find an approximate value for \(y\) when \(x = 1\).
Markscheme
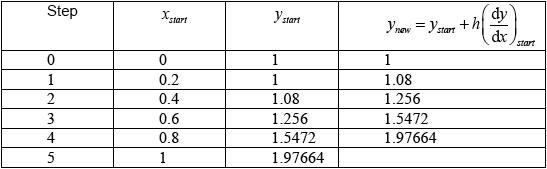 (M1)(A1)(A1)(A1)
(M1)(A1)(A1)(A1)
Note: Award M1 for equivalent of setting up first row of table, A1 for each of row 2, 3 and 5.
approximate solution \(y = 1.98\) A1
make the increments smaller or any specific correct instruction – for example change increment from \(0.2\) to \(0.1\) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} - y = 2x - 1\)
integrating factor is \({{\text{e}}^{\int { - 1{\text{d}}x} }} = {{\text{e}}^{ - x}}\) (M1)(A1)
\(\frac{{\text{d}}}{{{\text{d}}x}}(y{{\text{e}}^{ - x}}) = {{\text{e}}^{ - x}}(2x - 1)\) M1
attempt at integration by parts of \(\int {{{\text{e}}^{ - x}}(2x - 1){\text{d}}x} \) (M1)
\( = - (2x - 1){{\text{e}}^{ - x}} + \int {2{{\text{e}}^{ - x}}{\text{d}}x} \) A1
\( = - (2x - 1){{\text{e}}^{ - x}} - 2{{\text{e}}^{ - x}}( + c)\) A1
\(y{{\text{e}}^{ - x}} = - (1 + 2x){{\text{e}}^{ - x}} + c\)
\(y = - (1 + 2x) + c{{\text{e}}^x}\)
when \(x = 0,{\text{ }}y = 1 \Rightarrow c = 2\) M1
\(y = - (1 + 2x) + 2{{\text{e}}^{ - x}}\) A1
when \(x = 1,{\text{ }}y = - 3 + 2{\text{e}}\) A1
(i) METHOD 1
\(f(0) = 1,{\text{ }}f'(0) = 0\) A1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 + \frac{{{\text{d}}y}}{{{\text{d}}x}} \Rightarrow {f^2}(0) = 2\) A1
\(\frac{{{{\text{d}}^3}y}}{{{\text{d}}{x^3}}} = \frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} \Rightarrow {f^3}(0) = 2\) A1
hence \(y = 1 + {x^2} + \frac{{{x^3}}}{3} + \ldots \) A1
Note: Accuracy marks are independent of each other.
METHOD 2
using Maclaurin series for \({{\text{e}}^x} = 1 + x + \frac{{{x^2}}}{{2!}} + \frac{{{x^3}}}{{3!}} + \ldots \) M1
\(y = - 1 - 2x + 2\left( {1 + x + \frac{{{x^2}}}{{2!}} + \frac{{{x^3}}}{{3!}} + \ldots } \right)\) M1A1
\(y = 1 + {x^2} + \frac{{{x^3}}}{3} + \ldots \) A1
(ii) when \(x = 1,{\text{ }}y = 1 + 1 + \frac{1}{3} = \frac{7}{3} = 2.33\) A1
Examiners report
Most candidates were successful in applying Euler’s method and in explaining how it could be improved to provide a better approximation.
Most candidates were successful in applying Euler’s method and in explaining how it could be improved to provide a better approximation.
In part c) many candidates successfully used an integrating factor to solve the differential equation but a significant minority were unable to make a meaningful start.
Part d) produced many fully correct answers, but candidates sometimes used their own answers to part c) to derive the Maclaurin series rather than the given equation. In most cases this did not cause a problem but a small number of candidates produced an expression of such complexity that they were unable to differentiate to the required number of terms.

