| Date | May 2014 | Marks available | 13 | Reference code | 14M.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
(a) Consider the recurrence relation \(a{u_{n + 1}} + b{u_n} + c{u_{n - 1}} = 0\).
Show that \({u_n} = A{\lambda ^n} + B{\mu ^n}\) satisfies this relation where \(A\), \(B\) are arbitrary constants and \(\lambda \), \(\mu \) are the roots of the equation \(a{x^2} + bx + c = 0\).
(b) 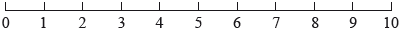
A particle \(P\) executes a random walk on the line above such that when it is at point \(n\left( {1 \leqslant n \leqslant 9,{\text{ }}n \in {\mathbb{Z}^ + }} \right)\) it has a probability \(0.4\) of moving to \(n + 1\) and a probability \(0.6\) of moving to \(n - 1\). The walk terminates as soon as \(P\) reaches either \(0\) or \(10\). Let \({p_n}\) denote the probability that the walk terminates at \(0\) starting from \(n\).
(i) Show that \(2{p_{n + 1}} - 5{p_n} + 3{p_{n - 1}} = 0\).
(ii) By solving this recurrence relation subject to the boundary conditions \({p_0} = 1\), \({p_{10}} = 0\) show that \({p_n} = \frac{{{{1.5}^{10}} - {{1.5}^n}}}{{{{1.5}^{10}} - 1}}\).
Markscheme
(a) consider
\(a{u_{n + 1}} + b{u_n} + c{u_{n - 1}} = aA{\lambda ^{n + 1}} + aB{\mu ^{n + 1}} + bA{\lambda ^n} + bB{\mu ^n} + cA{\lambda ^{n - 1}} + cB{\mu ^{n - 1}}\) M1A1
\( = A{\lambda ^{n - 1}}\left( {a{\lambda ^2} + b\lambda + c} \right) + B{\mu ^{n - 1}}\left( {a{\mu ^2} + b\mu + c} \right)\) A1
\(= 0 \)
[3 marks]
(b) (i) to terminate at \(0\) starting from \(n\), the particle must either move to \(n + 1\) and terminate at \(0\) starting from there or move to \(n - 1\) and terminate at \(0\) starting from there
therefore,
\({p_n} = 0.4{p_{n + 1}} + 0.6{p_{n - 1}}\) M1A2
leading to \(2{p_{n + 1}} - 5{p_n} + 3{p_{n - 1}} = 0\) AG
(ii) solving the auxiliary equation \(2{x^2} - 5x + 3 = 0\) M1
\(x = 1,{\text{ 1.5}}\) A1
the general solution is
\({p_n} = A + B{(1.5)^n}\) A1
substituting the boundary conditions,
\(A + B = 1\)
\(A + B{(1.5)^{10}} = 0\) M1A1
solving,
\(A = \frac{{{{1.5}^{10}}}}{{{{1.5}^{10}} - 1}};{\text{ }}B = - \frac{1}{{{{1.5}^{10}} - 1}}\) A1A1
giving
\({p_n} = \frac{{{{1.5}^{10}} - {{1.5}^n}}}{{{{1.5}^{10}} - 1}}\) AG
[10 marks]

