| Date | May 2017 | Marks available | 3 | Reference code | 17M.1.hl.TZ0.12 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Show that | Question number | 12 | Adapted from | N/A |
Question
The vertices A, B, C of an acute angled triangle have position vectors a, b, c with respect to an origin O.
The mid-point of [BC] is denoted by D. The point E lies on [AD] such that \({\text{AE}} = 2{\text{DE}}\).
The perpendiculars from B to [AC] and C to [AB] meet at the point F.
Show that the position vector of E is
\(\frac{1}{3}\) (a + b + c).
Explain briefly why this result shows that the three medians of a triangle are concurrent.
Show that the position vector f of F satisfies the equations
(b – f ) \( \bullet \) (c – a) = 0
(c – f ) \( \bullet \) (a – b) = 0.
Show, by expanding these equations, that
(a – f ) \( \bullet \) (c – b) = 0.
Explain briefly why this result shows that the three altitudes of a triangle are concurrent.
Markscheme
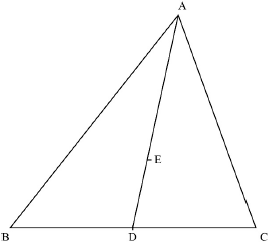
d = b + \(\frac{1}{2}\)(c – b) = \(\frac{1}{2}\)(b + c) (M1)A1
e = d + \(\frac{1}{3}\)(a – d) M1
= \(\frac{1}{2}\)(b + c) + \(\frac{1}{3}\)(a - \(\frac{1}{2}\)(b + c)) A1
= \(\frac{1}{3}\)(a + b + c) AG
[??? marks]
(because of the symmetry of the result), the other two medians also pass through E. R1
[??? marks]
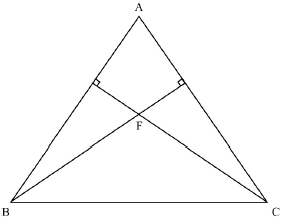
\(\overrightarrow {{\text{BF}}} \) = f – b and \(\overrightarrow {{\text{AC}}} \) = c – a A1
since FB is perpendicular to AC, (b – f) \( \bullet \) (c – a) = 0 R1AG
similarly since FC is perpendicular to BA, (c – f) \( \bullet \) (a – b) = 0 R1AG
[??? marks]
expanding these equations and adding, M1
b \( \bullet \) c – b \( \bullet \) a – f \( \bullet \) c + f \( \bullet \) a + c \( \bullet \) a – c \( \bullet \) b – f \( \bullet \) a + f \( \bullet \) b = 0 A1
– b \( \bullet \) a – f \( \bullet \) c + c \( \bullet \) a + f \( \bullet \) b = 0 A1
leading to (a – f) \( \bullet \) (c – b) = 0 AG
[??? marks]
this result shows that AF is perpendicular to BC so that the three altitudes are concurrent (at F) R1
[??? marks]

