| Date | May 2013 | Marks available | 6 | Reference code | 13M.1.hl.TZ0.3 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
A triangle \(T\) has sides of length \(3\), \(4\) and \(5\).
(i) Find the radius of the circumscribed circle of \(T\) .
(ii) Find the radius of the inscribed circle of \(T\) .
A triangle \(U\) has sides of length \(4\), \(5\) and \(7\).
(i) Show that the orthocentre, H, of \(U\) lies outside the triangle.
(ii) Show that the foot of the perpendicular from H to the longest side divides it in the ratio \(29:20\).
Markscheme
(i) \(T\) is a right angled triangle \( \Rightarrow \) the hypotenuse is a diameter (M1)
circumradius \( = 2.5\) A1
(ii) diagram seen with some sensible unknown(s) given (A1)

need to solve \(3 - r + 4 - r = 5\) (or equivalent) M1A1
\(r = 1\) A1
[6 marks]
(i) recognition that \({7^2} > {4^2} + {5^2}\) M1
therefore one of the angles is obtuse R1
so the orthocentre, H, of \(U\) lies outside of the triangle AG
(ii) foot of perpendicular from H to longest side is the foot of the perpendicular from A to the longest side (R1)
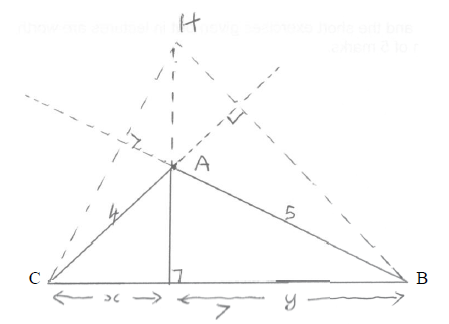
EITHER
attempt to solve \({4^2} - {x^2} = {5^2} - {(7 - x)^2}\) or \({4^2} - {(7 - y)^2} = {5^2} - {y^2}\) M1A1
obtain \(x = \frac{{20}}{7}\) or \(y = \frac{{29}}{7}\) A1
OR
if \(\hat B\) is the smallest angle
\(\cos \hat B = \frac{{25 + 49 - 16}}{{2 \times 5 \times 7}}\) M1
\( = \frac{{58}}{{70}} = \frac{{29}}{{35}}\)
\(y = 5 \times \frac{{29}}{{35}} = \frac{{29}}{7}\) A1
\(x = 7 - \frac{{29}}{7} = \frac{{20}}{7}\) A1
THEN
ratio \(29:20\) (accept \(20:29\)) AG
Note: Accept the use of Stewart’s theorem.
[6 marks]
Examiners report
A few fully correct answers were seen to this question, but many candidates were unable to make much progress after part a) (i) and a significant minority made no attempt at all. A few fully correct answers were seen to part a) (ii) and part b) (i). In both part a) (ii) and part b) (ii) a majority of candidates were unable to draw a meaningful diagram to enable them to start the question.
A few fully correct answers were seen to this question, but many candidates were unable to make much progress after part a) (i) and a significant minority made no attempt at all. A few fully correct answers were seen to part a) (ii) and part b) (i). In both part a) (ii) and part b) (ii) a majority of candidates were unable to draw a meaningful diagram to enable them to start the question.

