| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.sl.TZ1.15 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 15 | Adapted from | N/A |
Question
A cuboid has a rectangular base of width \(x\) cm and length 2\(x\) cm . The height of the cuboid is \(h\) cm . The total length of the edges of the cuboid is \(72\) cm.
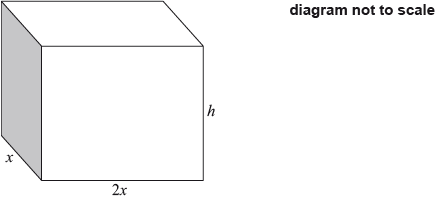
The volume, \(V\), of the cuboid can be expressed as \(V = a{x^2} - 6{x^3}\).
Find the value of \(a\).
Find the value of \(x\) that makes the volume a maximum.
Markscheme
\(72 = 12x + 4h\;\;\;\)(or equivalent) (M1)
Note: Award (M1) for a correct equation obtained from the total length of the edges.
\(V = 2{x^2}(18 - 3x)\) (A1)
\((a = ){\text{ }}36\) (A1) (C3)
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 72x - 18{x^2}\) (A1)
\(72x - 18{x^2} = 0\;\;\;\)OR\(\;\;\;\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) (M1)
Notes: Award (A1) for \( - 18{x^2}\) seen. Award (M1) for equating derivative to zero.
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Note: Follow through from part (a).
OR
Sketch of \(V\) with visible maximum (M1)
Sketch with \(x \geqslant 0,{\text{ }}V \geqslant 0\) and indication of maximum (e.g. coordinates) (A1)(ft)
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Notes: Follow through from part (a).
Award (M1)(A1)(A0) for \((4,{\text{ }}192)\).
Award (C3) for \(x = 4,{\text{ }}y = 192\).
Examiners report
The model in this question seemed to be too difficult for the vast majority of the candidates, and therefore was a strong discriminator between grade 6 and grade 7 candidates. An attempt to find an equation for the volume of the cube often started with V = x x 2x x h . Many struggled to translate the total length of the edges into a correct equation, and consequently were unable to substitute h. Some tried to write x in terms of h and got lost, others tried to work backwards from the expression given in the question.
As very few found a value for a, often part (b) was not attempted. When a derivative was calculated this was usually done correctly.

