| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.sl.TZ2.5 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
A parcel is in the shape of a rectangular prism, as shown in the diagram. It has a length \(l\) cm, width \(w\) cm and height of \(20\) cm.
The total volume of the parcel is \(3000{\text{ c}}{{\text{m}}^3}\).
Express the volume of the parcel in terms of \(l\) and \(w\).
Show that \(l = \frac{{150}}{w}\).
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
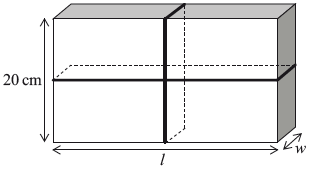
Show that the length of string, \(S\) cm, required to tie up the parcel can be written as
\[S = 40 + 4w + \frac{{300}}{w},{\text{ }}0 < w \leqslant 20.\]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Draw the graph of \(S\) for \(0 < w \leqslant 20\) and \(0 < S \leqslant 500\), clearly showing the local minimum point. Use a scale of \(2\) cm to represent \(5\) units on the horizontal axis \(w\) (cm), and a scale of \(2\) cm to represent \(100\) units on the vertical axis \(S\) (cm).
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find \(\frac{{{\text{d}}S}}{{{\text{d}}w}}\).
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the value of \(w\) for which \(S\) is a minimum.
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Write down the value, \(l\), of the parcel for which the length of string is a minimum.
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the minimum length of string required to tie up the parcel.
Markscheme
\(20lw\) OR \(V = 20lw\) (A1)
[1 mark]
\(3000 = 20lw\) (M1)
Note: Award (M1) for equating their answer to part (a) to \(3000\).
\(l = \frac{{3000}}{{20w}}\) (M1)
Note: Award (M1) for rearranging equation to make \(l\) subject of the formula. The above equation must be seen to award (M1).
OR
\(150 = lw\) (M1)
Note: Award (M1) for division by \(20\) on both sides. The above equation must be seen to award (M1).
\(l = \frac{{150}}{w}\) (AG)
[2 marks]
\(S = 2l + 4w + 2(20)\) (M1)
Note: Award (M1) for setting up a correct expression for \(S\).
\(2\left( {\frac{{150}}{w}} \right) + 4w + 2(20)\) (M1)
Notes: Award (M1) for correct substitution into the expression for \(S\). The above expression must be seen to award (M1).
\( = 40 + 4w + \frac{{300}}{w}\) (AG)
[2 marks]
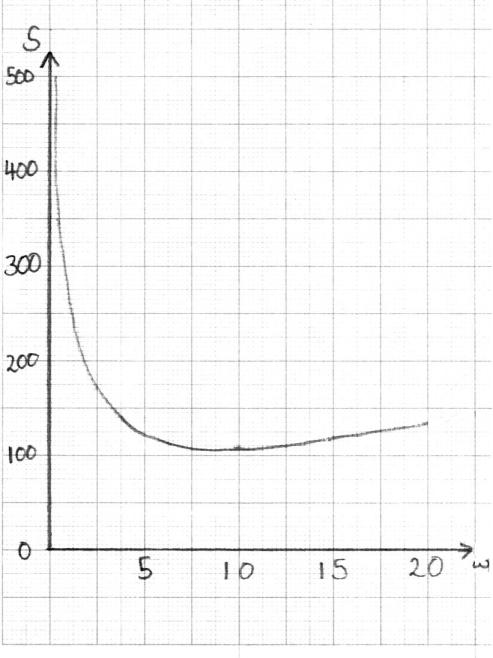 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Note: Award (A1) for correct scales, window and labels on axes, (A1) for approximately correct shape, (A1) for minimum point in approximately correct position, (A1) for asymptotic behaviour at \(w = 0\).
Axes must be drawn with a ruler and labeled \(w\) and \(S\).
For a smooth curve (with approximately correct shape) there should be one continuous thin line, no part of which is straight and no (one-to-many) mappings of \(w\).
The \(S\)-axis must be an asymptote. The curve must not touch the \(S\)-axis nor must the curve approach the asymptote then deviate away later.
[4 marks]
\(4 - \frac{{300}}{{{w^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(4\), (A1) for \(-300\), (A1) for \(\frac{1}{{{w^2}}}\) or \({w^{ - 2}}\). If extra terms present, award at most (A1)(A1)(A0).
[3 marks]
\(4 - \frac{{300}}{{{w^2}}} = 0\) OR \(\frac{{300}}{{{w^2}}} = 4\) OR \(\frac{{{\text{d}}S}}{{{\text{d}}w}} = 0\) (M1)
Note: Award (M1) for equating their derivative to zero.
\(w = 8.66{\text{ }}\left( {\sqrt {75} ,{\text{ 8.66025}} \ldots } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).
[2 marks]
\(17.3 \left( {\frac{{150}}{{\sqrt {75} }},{\text{ 17.3205}} \ldots } \right)\) (A1)(ft)
Note: Follow through from their answer to part (f).
[1 mark]
\(40 + 4\sqrt {75} + \frac{{300}}{{\sqrt {75} }}\) (M1)
Note: Award (M1) for substitution of their answer to part (f) into the expression for \(S\).
\( = 110{\text{ (cm) }}\left( {40 + 40\sqrt 3 ,{\text{ 109.282}} \ldots } \right)\) (A1)(ft)(G2)
Note: Do not accept \(109\).
Follow through from their answers to parts (f) and (g).
[2 marks]

