| Date | May 2014 | Marks available | 1 | Reference code | 14M.1.sl.TZ2.13 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 13 | Adapted from | N/A |
Question
Consider the graph of the function \(f(x) = {x^3} + 2{x^2} - 5\).
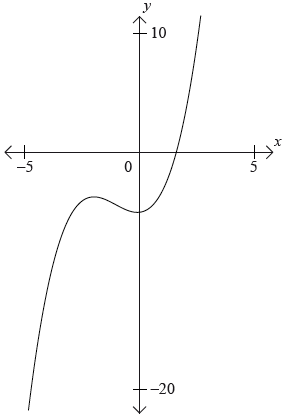
Label the local maximum as \({\text{A}}\) on the graph.
[1]
a.
Label the local minimum as B on the graph.
[1]
b.
Write down the interval where \(f'(x) < 0\).
[1]
c.
Draw the tangent to the curve at \(x = 1\) on the graph.
[1]
d.
Write down the equation of the tangent at \(x = 1\).
[2]
e.
Markscheme
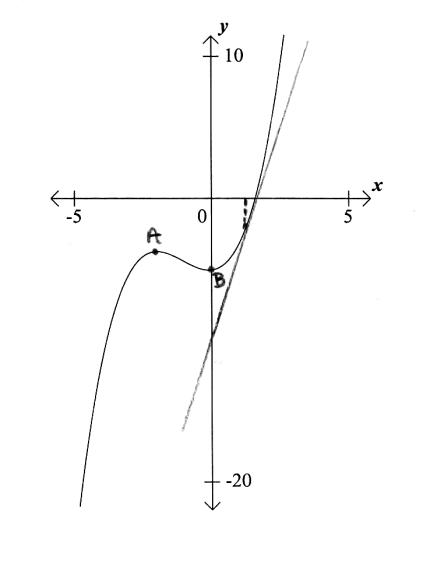
correct label on graph (A1) (C1)
[1 mark]
a.
correct label on graph (A1) (C1)
[1 mark]
b.
\( - 1.33 < x < 0\) \(\left( { - \frac{4}{3} < x < 0} \right)\) (A1) (C1)
[1 mark]
c.
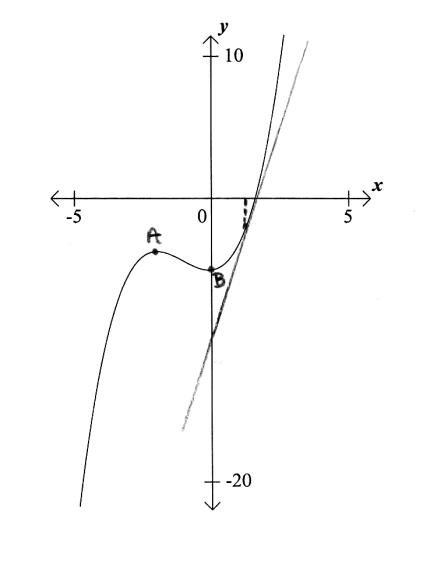
tangent drawn at \(x = 1\) on graph (A1) (C1)
[1 mark]
d.
\(y = 7x - 9\) (A1)(A1) (C2)
Notes: Award (A1) for \(7\), (A1) for \(-9\).
If answer not given as an equation award at most (A1)(A0).
[2 marks]
e.
Examiners report
[N/A]
a.
[N/A]
b.
[N/A]
c.
[N/A]
d.
[N/A]
e.
