| Date | None Specimen | Marks available | 4 | Reference code | SPNone.1.sl.TZ0.1 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Express | Question number | 1 | Adapted from | N/A |
Question
In the following diagram, \(\boldsymbol{u} = \overrightarrow {{\rm{AB}}} \) and \(\boldsymbol{v} = \overrightarrow {{\rm{BD}}} \) .
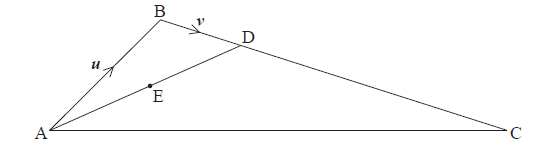
The midpoint of \(\overrightarrow {{\rm{AD}}} \) is E and \(\frac{{{\rm{BD}}}}{{{\rm{DC}}}} = \frac{1}{3}\) .
Express each of the following vectors in terms of \(\boldsymbol{u}\) and \(\boldsymbol{v}\) .
\(\overrightarrow {{\rm{AE}}} \)
\(\overrightarrow {{\rm{EC}}} \)
Markscheme
\(\overrightarrow {{\rm{AE}}} = \frac{1}{2}\overrightarrow {{\rm{AD}}} \) A1
attempt to find \(\overrightarrow {{\rm{AD}}} \) M1
e.g. \(\overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{BD}}} \) , \({\boldsymbol{u}} + {\boldsymbol{v}}\)
\(\overrightarrow {{\rm{AE}}} = \frac{1}{2}(u + v)\) \(\left( { = \frac{1}{2}{\boldsymbol{u}} + \frac{1}{2}{\boldsymbol{v}}} \right)\) A1 N2
[3 marks]
\(\overrightarrow {{\rm{EC}}} = \overrightarrow {{\rm{AE}}} = \frac{1}{2}({\boldsymbol{u}} + {\boldsymbol{v}})\) A1
\(\overrightarrow {{\rm{DC}}} = 3{\boldsymbol{v}}\) A1
attempt to find \(\overrightarrow {{\rm{EC}}} \) M1
e.g. \(\overrightarrow {{\rm{ED}}} + \overrightarrow {{\rm{DC}}} \) , \(\frac{1}{2}({\boldsymbol{u}} + {\boldsymbol{v}}) + 3{\boldsymbol{v}}\)
\(\overrightarrow {{\rm{EC}}} = \frac{1}{2}{\boldsymbol{u}} + \frac{7}{2}{\boldsymbol{v}}\) \(\left( { = \frac{1}{2}({\boldsymbol{u}} + 7{\boldsymbol{v}})} \right)\) A1 N2
[4 marks]

