| Date | November 2013 | Marks available | 3 | Reference code | 13N.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Hence and Sketch | Question number | 8 | Adapted from | N/A |
Question
Let \(f(x) = 3x - 2\) and \(g(x) = \frac{5}{{3x}}\), for \(x \ne 0\).
Let \(h(x) = \frac{5}{{x + 2}}\), for \(x \geqslant 0\). The graph of h has a horizontal asymptote at \(y = 0\).
Find \({f^{ - 1}}(x)\).
Show that \(\left( {g \circ {f^{ - 1}}} \right)(x) = \frac{5}{{x + 2}}\).
Find the \(y\)-intercept of the graph of \(h\).
Hence, sketch the graph of \(h\).
For the graph of \({h^{ - 1}}\), write down the \(x\)-intercept;
For the graph of \({h^{ - 1}}\), write down the equation of the vertical asymptote.
Given that \({h^{ - 1}}(a) = 3\), find the value of \(a\).
Markscheme
interchanging \(x\) and \(y\) (M1)
eg \(x = 3y - 2\)
\({f^{ - 1}}(x) = \frac{{x + 2}}{3}{\text{ }}\left( {{\text{accept }}y = \frac{{x + 2}}{3},{\text{ }}\frac{{x + 2}}{3}} \right)\) A1 N2
[2 marks]
attempt to form composite (in any order) (M1)
eg \(g\left( {\frac{{x + 2}}{3}} \right),{\text{ }}\frac{{\frac{5}{{3x}} + 2}}{3}\)
correct substitution A1
eg \(\frac{5}{{3\left( {\frac{{x + 2}}{3}} \right)}}\)
\(\left( {g \circ {f^{ - 1}}} \right)(x) = \frac{5}{{x + 2}}\) AG N0
[2 marks]
valid approach (M1)
eg \(h(0),{\text{ }}\frac{5}{{0 + 2}}\)
\(y = \frac{5}{2}{\text{ }}\left( {{\text{accept (0, 2.5)}}} \right)\) A1 N2
[2 marks]
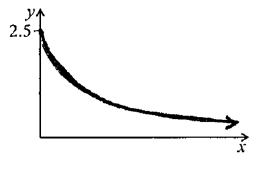 A1A2 N3
A1A2 N3
Notes: Award A1 for approximately correct shape (reciprocal, decreasing, concave up).
Only if this A1 is awarded, award A2 for all the following approximately correct features: y-intercept at \((0, 2.5)\), asymptotic to x-axis, correct domain \(x \geqslant 0\).
If only two of these features are correct, award A1.
[3 marks]
\(x = \frac{5}{2}{\text{ }}\left( {{\text{accept (2.5, 0)}}} \right)\) A1 N1
[1 mark]
\(x = 0\) (must be an equation) A1 N1
[1 mark]
METHOD 1
attempt to substitute \(3\) into \(h\) (seen anywhere) (M1)
eg \(h(3),{\text{ }}\frac{5}{{3 + 2}}\)
correct equation (A1)
eg \(a = \frac{5}{{3 + 2}},{\text{ }}h(3) = a\)
\(a = 1\) A1 N2
[3 marks]
METHOD 2
attempt to find inverse (may be seen in (d)) (M1)
eg \(x = \frac{5}{{y + 2}},{\text{ }}{h^{ - 1}} = \frac{5}{x} - 2,{\text{ }}\frac{5}{x} + 2\)
correct equation, \(\frac{5}{x} - 2 = 3\) (A1)
\(a = 1\) A1 N2
[3 marks]

