 20% of the world's deserts covered with solar panels would supply enough energy for present needs. Here we will learn the first half of a means to calculate this energy: the intensity of the light emitted from the Sun upon the Earth's surface.
20% of the world's deserts covered with solar panels would supply enough energy for present needs. Here we will learn the first half of a means to calculate this energy: the intensity of the light emitted from the Sun upon the Earth's surface.
Key Concepts
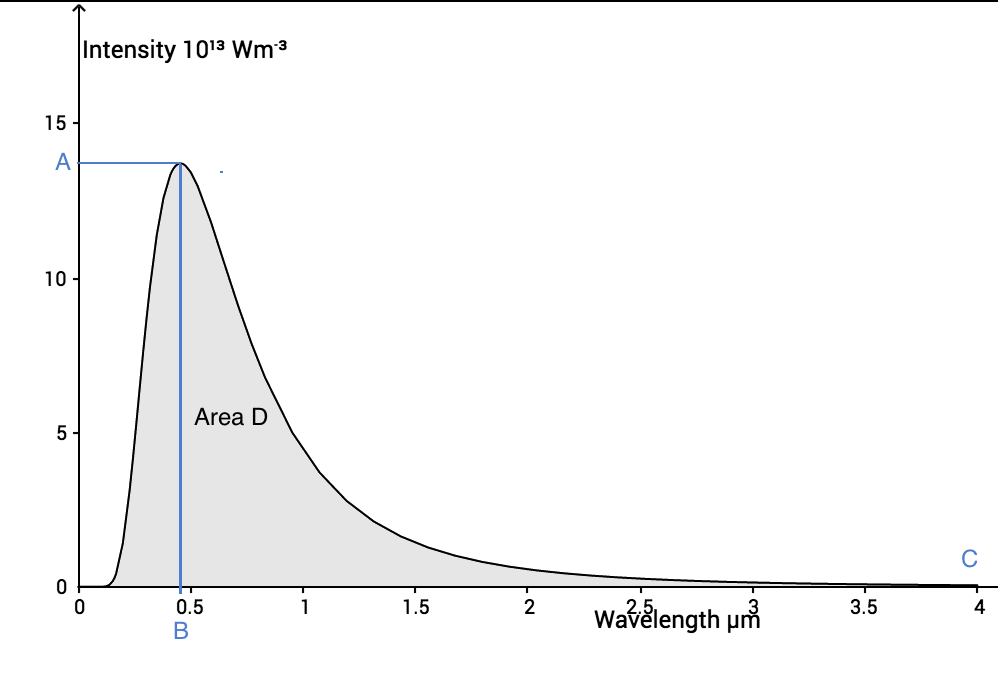
The higher the temperature, the larger the area of the black body curve above the axis, as this is proportional to the total power emitted. The Stefan Boltzmann law gives the relationship between temperature and power emitted per unit area:
\(P=e\sigma AT^4\)
- P = power released (W)
- e = emissivity (dimensionless quantity = 1 for a black body)
- σ = constant of proportionality
- A = surface area (m2)
- T = absolute temperature (K)
NB: It is worth taking note of the power of 4, making the temperature of the body much more significant in determining the power than the area.
How much of Energy from the Sun have you understood?


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn