IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	2	Reference code	17M.1.SL.TZ2.T_4
Level	Standard Level	Paper	Paper 1 (with calculator from previous syllabus)	Time zone	Time zone 2
Command term	Find	Question number	T_4	Adapted from	N/A

Question

Line $L$ intersects the $x$ -axis at point A and the $y$ -axis at point B, as shown on the diagram.

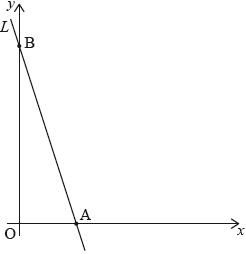
M17/5/MATSD/SP1/ENG/TZ2/04

The length of line segment OB is three times the length of line segment OA, where O is the origin.

Point ${\text{(2, 6)}}$ lies on $L$ .

Find the equation of $L$ in the form $y = mx + c$ .

[2]

Find the $x$ -coordinate of point A.

[2]

Markscheme

$6 = - 3(2) + c$ $\,\,\,$ OR $\,\,\,$ $(y - 6) = - 3(x - 2)$ (M1)

Note: Award (M1) for substitution of their gradient from part (a) into a correct equation with the coordinates $(2,{\text{ }}6)$ correctly substituted.

$y = - 3x + 12$ (A1)(ft) (C2)

Notes: Award (A1)(ft) for their correct equation. Follow through from part (a).

If no method seen, award (A1)(A0) for $y = - 3x$ .

Award (A1)(A0) for $- 3x + 12$ .

[2 marks]

$0 = - 3x + 12$ (M1)

Note: Award (M1) for substitution of $y = 0$ in their equation from part (b).

$(x = ){\text{ }}4$ (A1)(ft) (C2)

Notes: Follow through from their equation from part (b). Do not follow through if no method seen. Do not award the final (A1) if the value of $x$ is negative or zero.

[2 marks]

Examiners report

[N/A]

Syllabus sections

Topic 2—Functions » SL 2.1—Equations of straight lines, parallel and perpendicular

22M.1.SL.TZ1.1a:
Find the equation of $L$ .
22M.2.SL.TZ2.3b:
Assuming Kaia’s annual salary can be approximately modelled by the equation $S = a x + b$ , show that Kaia had a higher salary than Gemma in the year 2021, according to the model.
21N.1.SL.TZ0.5b:
Find $f (4)$ .
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).

Give your answer in the form y = mx + c.
18N.2.SL.TZ0.T_4c:
Sketch the graph of the function g (x) = 10x + 40 on the same axes.
21N.1.SL.TZ0.5a:
Write down the value of $f' (4)$ .
22M.1.SL.TZ1.1b:
The line $L$ passes through the point $(k, 2)$ .

Find the value of $k$ .
22M.1.SL.TZ2.7c:
Find the equation of $L$ .
21N.1.SL.TZ0.5c:
Find $h (4)$ .
17M.1.SL.TZ2.T_4b:
Find the equation of $L$ in the form $y = mx + c$ .
21N.1.SL.TZ0.5d:
Hence find the equation of the tangent to the graph of $h$ at $x = 4$ .

Topic 2—Functions

Question

Markscheme

Examiners report

Syllabus sections

View options