| Date | May 2018 | Marks available | 1 | Reference code | 18M.2.HL.TZ1.3 |
| Level | Higher level | Paper | Paper 2 | Time zone | 1 |
| Command term | Outline | Question number | 3 | Adapted from | N/A |
Question
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
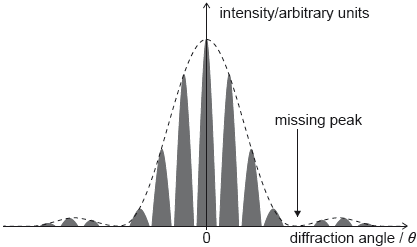
The graph of variation of intensity with diffraction angle for this experiment is shown.
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.

A series of dark and bright fringes appears on the screen. Explain how a dark fringe is formed.
Outline why the beam has to be coherent in order for the fringes to be visible.
The wavelength of the beam as observed on Earth is 633.0 nm. The separation between a dark and a bright fringe on the screen is 4.50 mm. Calculate D.
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.
Deduce, in mm, the width of one slit.
The wavelength of the light in the beam when emitted by the galaxy was 621.4 nm.
Explain, without further calculation, what can be deduced about the relative motion of the galaxy and the Earth.
Markscheme
superposition of light from each slit / interference of light from both slits
with path/phase difference of any half-odd multiple of wavelength/any odd multiple of (in words or symbols)
producing destructive interference
Ignore any reference to crests and troughs.
[3 marks]
light waves (from slits) must have constant phase difference / no phase difference / be in phase
OWTTE
[1 mark]
evidence of solving for D «D » ✔
«» = 4.27 «m» ✔
Award [1] max for 2.13 m.
sin θ =
sin θ = 0.0084401…
final answer to three sig figs (eg 0.00844 or 8.44 × 10–3)
Allow ECF from (a)(iii).
Award [1] for 0.121 rad (can award MP3 in addition for proper sig fig)
Accept calculation in degrees leading to 0.481 degrees.
Award MP3 for any answer expressed to 3sf.
[3 marks]
use of diffraction formula «b = »
OR
«=» 7.5«00» × 10–2 «mm»
Allow ECF from (b)(i).
[2 marks]
wavelength increases (so frequency decreases) / light is redshifted
galaxy is moving away from Earth
Allow ECF for MP2 (ie wavelength decreases so moving towards).
[2 marks]

