| Date | May 2018 | Marks available | 2 | Reference code | 18M.3.SL.TZ2.1 |
| Level | Standard level | Paper | Paper 3 | Time zone | 2 |
| Command term | Estimate and Determine | Question number | 1 | Adapted from | N/A |
Question
To determine the acceleration due to gravity, a small metal sphere is dropped from rest and the time it takes to fall through a known distance and open a trapdoor is measured.
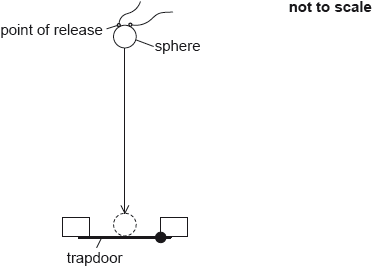
The following data are available.
Determine the distance fallen, in m, by the centre of mass of the sphere including an estimate of the absolute uncertainty in your answer.
Using the following equation
calculate, for these data, the acceleration due to gravity including an estimate of the absolute uncertainty in your answer.
Markscheme
distance fallen = 654 – 12 = 642 «mm»
absolute uncertainty = 2 + 0.1 «mm» ≈ 2 × 10–3 «m» or = 2.1 × 10–3 «m» or 2.0 × 10–3 «m»
Accept answers in mm or m
[2 marks]
«a = » = 9.744 «ms–2»
fractional uncertainty in distance = AND fractional uncertainty in time =
total fractional uncertainty = «= 0.00311 + 2 × 0.00551»
total absolute uncertainty = 0.1 or 0.14 AND same number of decimal places in value and uncertainty, ie: 9.7 ± 0.1 or 9.74 ± 0.14
Accept working in % for MP2 and MP3
Final uncertainty must be the absolute uncertainty
[4 marks]

