| Date | November 2015 | Marks available | 3 | Reference code | 15N.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The data of the goals scored by players in a football club during a season are given in the following table.
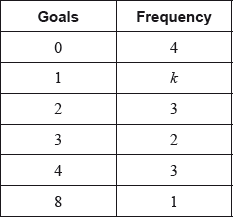
Given that the mean number of goals scored per player is \(1.95\) , find the value of \(k\).
It is discovered that there is a mistake in the data and that the top scorer, who scored 22 goals, has not been included in the table.
(i) Find the correct mean number of goals scored per player.
(ii) Find the correct standard deviation of the number of goals scored per player.
Markscheme
\(\frac{{0 \bullet 4 + 1 \bullet k + 2 \bullet 3 + 3 \bullet 2 + 4 \bullet 3 + 8 \bullet 1}}{{13 + k}} = 1.95\;\;\;\left( {\frac{{k + 32}}{{k + 13}} = 1.95} \right)\) (M1)
attempting to solve for \(k\) (M1)
\(k = 7\) A1
[3 marks]
(i) \(\frac{{7 + 32 + 22}}{{7 + 13 + 1}} = 2.90\;\;\;\left( { = \frac{{61}}{{21}}} \right)\) (M1)A1
(ii) standard deviation \( = 4.66\) A1
Note: Award A0 for \(4.77\).
[3 marks]
Total [6 marks]

