| Date | May 2014 | Marks available | 6 | Reference code | 14M.1.hl.TZ2.11 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Determine, Find, and Copy and complete | Question number | 11 | Adapted from | N/A |
Question
Mobile phone batteries are produced by two machines. Machine A produces 60% of the daily output and machine B produces 40%. It is found by testing that on average 2% of batteries produced by machine A are faulty and 1% of batteries produced by machine B are faulty.
(i) Draw a tree diagram clearly showing the respective probabilities.
(ii) A battery is selected at random. Find the probability that it is faulty.
(iii) A battery is selected at random and found to be faulty. Find the probability that it was produced by machine A.
In a pack of seven transistors, three are found to be defective. Three transistors are selected from the pack at random without replacement. The discrete random variable X represents the number of defective transistors selected.
(i) Find \({\text{P}}(X = 2)\).
(ii) Copy and complete the following table:

(iii) Determine \({\text{E}}(X)\).
Markscheme
(i)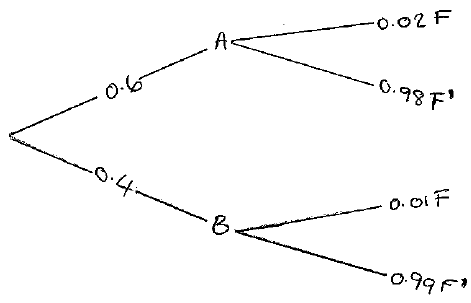 A1A1
A1A1
Note: Award A1 for a correctly labelled tree diagram and A1 for correct probabilities.
(ii) \({\text{P}}(F) = 0.6 \times 0.02 + 0.4 \times 0.01\) (M1)
\( = 0.016\) A1
(iii) \({\text{P}}(A|F) = \frac{{{\text{P}}(A \cap F)}}{{{\text{P}}(F)}}\)
\( = \frac{{0.6 \times 0.02}}{{0.016}}{\text{ }}\left( { = \frac{{0.012}}{{0.016}}} \right)\) M1
\( = 0.75\) A1
[6 marks]
(i) METHOD 1
\({\text{P}}(X = 2) = \frac{{^3{C_2}{ \times ^4}{C_1}}}{{^7{C_3}}}\) (M1)
\( = \frac{{12}}{{35}}\) A1
METHOD 2
\(\frac{3}{7} \times \frac{2}{6} \times \frac{4}{5} \times 3\) (M1)
\( = \frac{{12}}{{35}}\) A1
(ii)  A2
A2
Note: Award A1 if \(\frac{4}{{35}},{\text{ }}\frac{{18}}{{35}}\) or \(\frac{1}{{35}}\) is obtained.
(iii) \({\text{E}}(X) = \sum {x{\text{P}}(X = x)} \)
\({\text{E}}(X) = 0 \times \frac{4}{{35}} + 1 \times \frac{{18}}{{35}} + 2 \times \frac{{12}}{{35}} + 3 \times \frac{1}{{35}}\) M1
\( = \frac{{45}}{{35}} = \left( {\frac{9}{7}} \right)\) A1
[6 marks]

