| Date | May 2016 | Marks available | 2 | Reference code | 16M.1.hl.TZ1.3 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows the curve \(y = a\sin \left( {b(x + c)} \right) + d\), where \(a\), \(b\), \(c\) and \(d\) are all positive constants. The curve has a maximum point at \((1,{\text{ }}3.5)\) and a minimum point at \((2,{\text{ }}0.5)\).
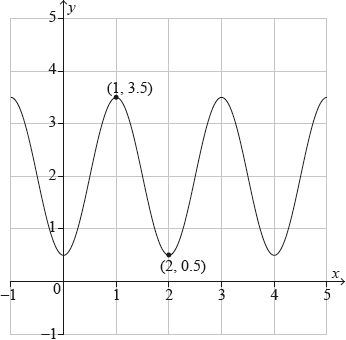
Write down the value of \(a\) and the value of \(d\).
Find the value of \(b\).
Find the smallest possible value of \(c\), given \(c > 0\).
Markscheme
\(a = 1.5\,\,\,d = 2\) A1A1
[2 marks]
\(b = \frac{{2\pi }}{2} = \pi \) (M1)A1
[2 marks]
attempt to solve an appropriate equation or apply a horizontal translation (M1)
\(c = 1.5\) A1
Note: Do not award a follow through mark for the final A1.
Award (M1)A0 for \(c = - 0.5\).
[2 marks]
Examiners report
Parts (a) and (b) were largely done successfully, but there was still a large minority who did not score well, and this is something that teachers need to be aware of for the future.
Parts (a) and (b) were largely done successfully, but there was still a large minority who did not score well, and this is something that teachers need to be aware of for the future.
This part was less successfully done. Some attempted the question by putting in a point and solving the equation. Others did it through realizing it represented a horizontal translation. Of these many failed to heed the instruction (given in the stem of the question, as well as repeated in part (c)) that \(c\) had to be greater than zero.

