| Date | November 2014 | Marks available | 2 | Reference code | 14N.3.HL.TZ0.4 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Discuss | Question number | 4 | Adapted from | N/A |
Question
This question is about the Hertzsprung–Russell (HR) diagram and stellar evolution.
The star Phi-1 Orionis is a large star on the main sequence with a mass of approximately 18 solar masses.
Calculate the luminosity of Phi-1 Orionis in terms of the luminosity of the Sun. Assume that \(n = 3.5\) in the mass–luminosity relation.
The Sun is expected to have a lifespan of around \({\text{1}}{{\text{0}}^{{\text{10}}}}\) years. With reference to the equilibrium between radiation pressure and gravitational pressure, discuss why Phi-1 Orionis will use up its hydrogen at a faster rate than the Sun.
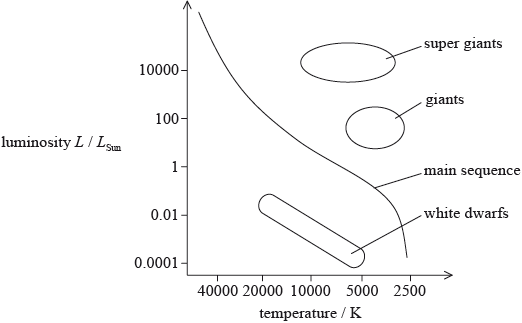
Using the HR diagram on page 6, draw the evolutionary path of Phi-1 Orionis as it leaves the main sequence.
Outline, with reference to the Oppenheimer–Volkoff limit, the fate of Phi-1 Orionis.
Markscheme
\(\frac{L}{{{L_\odot }}} = \left( {{{\left[ {\frac{m}{{{m_\odot }}}} \right]}^{3.5}} = } \right){\left[ {\frac{{18{m_\odot }}}{{{m_\odot }}}} \right]^{3.5}}\);
\(L = 25000{\text{ }}{L_\odot }\);
Answer must include \({L_\odot }\) in correct place.
Phi-1 Orionis has a larger mass so it has a larger gravitational pressure;
to remain in equilibrium it requires (an equal) radiation pressure which is provided by burning (hydrogen) at a faster rate;
line drawn starting from the top-left of the main sequence towards (red) super giants; } (allow anywhere within the grey shaded regions)
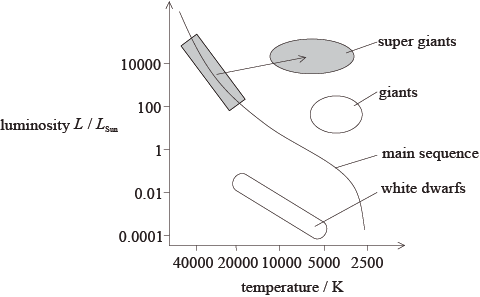
(mass of star is more than 15 solar masses so can be predicted, that) after supernova explosion it will be more than 3 solar masses/Oppenheimer-Volkoff limit and become a black hole;
or
if the mass after supernova explosion will be less than then Oppenheimer-Volkoff limit, it will become a neutron star;
Examiners report
This question was not easy. The majority of candidates calculated the luminosity of the star and used the balance between radiation pressure and gravitational pressure. Stronger candidates identified the evolution of the star on the HR diagram and showed the ability to distinguish between a black hole and neutron star.
This question was not easy. The majority of candidates calculated the luminosity of the star and used the balance between radiation pressure and gravitational pressure. Stronger candidates identified the evolution of the star on the HR diagram and showed the ability to distinguish between a black hole and neutron star.
This question was not easy. The majority of candidates calculated the luminosity of the star and used the balance between radiation pressure and gravitational pressure. Stronger candidates identified the evolution of the star on the HR diagram and showed the ability to distinguish between a black hole and neutron star.
This question was not easy. The majority of candidates calculated the luminosity of the star and used the balance between radiation pressure and gravitational pressure. Stronger candidates identified the evolution of the star on the HR diagram and showed the ability to distinguish between a black hole and neutron star.

