| Date | May 2018 | Marks available | 1 | Reference code | 18M.3.SL.TZ2.12 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Identify | Question number | 12 | Adapted from | N/A |
Question
Data from distant galaxies are shown on the graph.
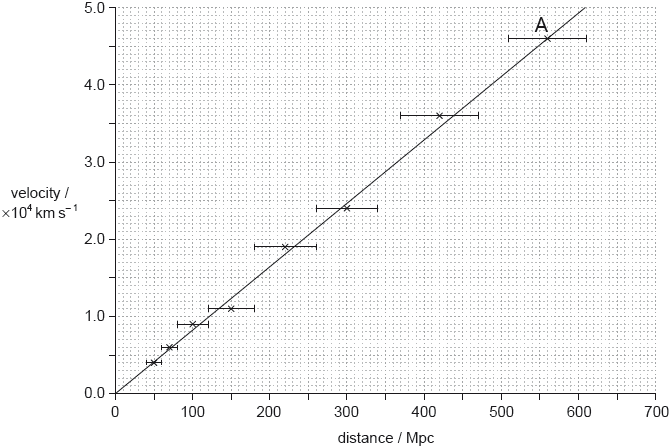
Estimate, using the data, the age of the universe. Give your answer in seconds.
Identify the assumption that you made in your answer to (a).
On the graph, one galaxy is labelled A. Determine the size of the universe, relative to its present size, when light from the galaxy labelled A was emitted.
Markscheme
use of gradient or any coordinate pair to find H0 «= \(\frac{v}{d}\)» or \(\frac{1}{{{H_0}}}\) «= \(\frac{d}{v}\)»
convert Mpc to m and km to m «for example \(\frac{{82 \times {{10}^3}}}{{{{10}^6} \times 3.26 \times 9.46 \times {{10}^{15}}}}\)»
age of universe «= \(\frac{1}{{{H_0}}}\)» = 3.8 × 1017 «s»
Allow final answers between
3.7 × 1017 and 3.9 × 1017 «s» or 4 × 1017 «s»
[3 marks]
non-accelerated/uniform rate of expansion
OR
H0 constant over time
OWTTE
[1 mark]
z « = \(\frac{v}{c}\)» = \(\frac{{4.6 \times {{10}^4} \times {{10}^3}}}{{3.00 \times {{10}^8}}}\) = 0.15
\(\frac{R}{{{R_0}}}\) = «z + 1» = 1.15
\(\frac{{{R_0}}}{R}\) = «\(\frac{1}{{1.15}}\) =» 0.87
OR
87% of the present size
[3 marks]

