| Date | None Specimen | Marks available | 9 | Reference code | SPNone.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Deduce, Hence, and Show that | Question number | 6 | Adapted from | N/A |
Question
A connected planar graph has \(e\) edges, \(f\) faces and \(v\) vertices. Prove Euler’s relation, that is \(v + f = e + 2\) .
(i) A simple connected planar graph with \(v\) vertices, where \(v \ge 3\) , has no circuit of length \(3\). Deduce that \(e \ge 2f\) and therefore that \(e \le 2v - 4\).
(ii) Hence show that \({\kappa _{3,3}}\) is non-planar.
The graph \(P\) has the following adjacency table, defined for vertices A to H, where each element represents the number of edges between the respective vertices.
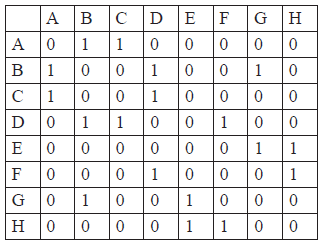
(i) Show that \(P\) is bipartite.
(ii) Show that the complement of \(P\) is connected but not planar.
Markscheme
consider the basic graph with just \(1\) vertex for which \(v = 1\) , \(f = 1\) and \(e = 0\)
for this case, \(v + f = e + 2 = 2\) so the result is true here M1A1
Note: Allow solutions which begin with a graph containing \(2\) vertices and an edge joining them for which \(v = 2\) , \(f = 1\) and \(e = 1\) .
a graph can be extended as follows – there are three cases to consider
I – an extra edge is added joining two distinct existing vertices R1
II – an extra edge is added joining an existing vertex to itself, forming a loop R1
in each case v remains the same and \(f\) and \(e\) each increase by \(1\)
both sides of the equation increase by \(1\) and the equation still holds R1
III – an extra vertex is added together with an edge joining this new vertex to an existing vertex (which is necessary to keep the graph connected) R1
in this case, \(f\) remains the same and \(v\) and \(e\) each increase by \(1\)
both sides of the equation increase by \(1\) and the equation still holds R1
any graph can be constructed from the basic graph by combining these operations, all of which result in Euler’s relation remaining valid R1
[8 marks]
(i) since the graph is simple there are no loops and no multiple edges and thus no circuits of length \(1\) or \(2\) R1
as we are told that there are no circuits of length 3, any face must be surrounded by at least \(4\) edges R1
since every edge is adjacent to \(2\) faces, R1
\(2e = \sum {({\text{degrees of faces}}) \ge 4f} \) , A1
it follows that \(e \ge 2f\) AG
using Euler’s relation with \(f \le \frac{e}{2}\) , M1
\(f = e - v + 2 \le \frac{e}{2}\) A1
giving \(e \le 2v - 4\) AG
(ii) \({\kappa _{3,3}}\) is simple and since it is bipartite it has no cycles of length \(3\) R1
for \({\kappa _{3,3}}\) , \(v = 6\) and \(e = 9\) A1
\(2v - 4 = 8\) so that the above inequality is not satisfied R1
it follows that \({\kappa _{3,3}}\) is not planar AG
[9 marks]
(i) attempt to find disjoint sets of vertices (M1)
disjoint sets are {A, D, G, H} and {B, C, E, F} A1
Note: Accept graph with vertices coloured, or otherwise annotated.
(ii) let \(P'\) denote the complement of P
in \(P'\) , A is connected to D, E, F, G and H : B and C are connected to E
therefore A is connected to all other vertices so \(P'\) is connected M1A1
a complete graph with \(8\) vertices has \(28\) edges A1
since \(P\) has \(9\) edges, \(P'\) has \(19\) edges A1
consider \(e \le 3v - 6\) (the condition for a planar graph) M1
for \({P'}\) , \(e = 19\) ; \(3v - 6 = 18\) so the condition is not satisfied A1
therefore \({P'}\) is not planar AG
[8 marks]

