| Date | May 2012 | Marks available | 2 | Reference code | 12M.1.hl.TZ0.2 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Express | Question number | 2 | Adapted from | N/A |
Question
Express the number \(47502\) as a product of its prime factors.
The positive integers \(M\) , \(N\) are such that \(\gcd (M,N) = 63\) and \(lcm(M,N) = 47502\) . Given that \(M\) is even and \(M < N\) , find the two possible pairs of values for \(M\) , \(N\) .
Markscheme
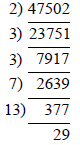 (M1)
(M1)
therefore \(47502 = 2 \times {3^2} \times 7 \times 13 \times 29\) A1
[2 marks]
noting that \(MN = \gcd \times {\rm{lcm}} = 2 \times {3^4} \times {7^2} \times 13 \times 29\) (M1)
the possibilities are
\((M,N) = (126,23751)\) A1A1
\((M,N) = (1638,1827)\) A1A1
[5 marks]
Examiners report
As expected, the factorization in (a) was successfully completed by most candidates.
Part (b) caused problems for some candidates. The most common mistake was that only one pair of values for \(M\), \(N\) was given.

