| Date | May 2007 | Marks available | 12 | Reference code | 07M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Determine, Explain, Find, Hence, and Write down | Question number | 1 | Adapted from | N/A |
Question
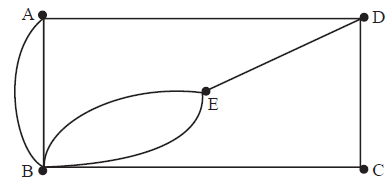
The diagram above shows the graph \(G\).
(i) Explain briefly why \(G\) has no Eulerian circuit.
(ii) Determine whether or not \(G\) is bipartite.
(iii) Write down the adjacency matrix of G. Hence find the number of walks of length \(4\) beginning at A and ending at C.
The cost adjacency matrix of a graph with vertices P, Q, R, S, T, U is given by
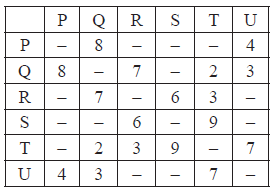
Use Dijkstra’s Algorithm to find the length of the shortest path between the vertices P and S. Show all the steps used by the algorithm and list the order of the vertices in the path.
Markscheme
(i) Because the graph has vertices of odd degree. R2
(ii) We are looking for \(2\) disjoint sets. (M1)
Put A in Set 1. Then B and D have to go in Set 2. This means that E and C have to go in Set 1. Therefore the disjoint sets are \(\left\{ {{\rm{B,D}}} \right\}\) and \(\left\{ {{\rm{A,C,E}}} \right\}\) . All the edges join a vertex from one set to a vertex in the other set. R2
The graph is bipartite. A1
(iii)
\({\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}}
0&2&0&1&0 \\
2&0&1&0&2 \\
0&1&0&1&0 \\
1&0&1&0&1 \\
0&2&0&1&0
\end{array}} \right)\)
We require the (\(1\), \(3\)) or (\(3\), \(1\)) element of \({\boldsymbol{M}^4}\) . M1M1
Using a GDC, the number of walks of length \(4\) is \(36\). A2
[12 marks]

The length of the shortest path is \(18\). A2
EITHER
P U Q T R S A2
OR
P U Q T S A2
[12 marks]

