| Date | May 2008 | Marks available | 3 | Reference code | 08M.1.hl.TZ0.2 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Solve | Question number | 2 | Adapted from | N/A |
Question
The group \(\left\{ {G,\left. * \right\}} \right.\) is defined on the set \(G = \left\{ {1,2,3,4,5,\left. 6 \right\}} \right.\) where \( * \) denotes multiplication modulo \(7\).
Draw the Cayley table for \(\left\{ {G,\left. * \right\}} \right.\) .
(i) Determine the order of each element of \(\left\{ {G,\left. * \right\}} \right.\) .
(ii) Find all the proper subgroups of \(\left\{ {G,\left. * \right\}} \right.\) .
Solve the equation \(x * 6 * x = 3\) where \(x \in G\) .
Markscheme
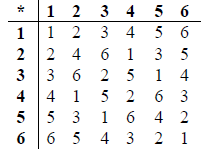 A3
A3
Note: Award A2 for 1 error, A1 for 2 errors, A0 for 3 or more errors.
[3 marks]
(i) We first identify \(1\) as the identity (A1)
Order of \(1 = 1\)
Order of \(2 = 3\)
Order of \(3 = 6\)
Order of \(4 = 3\)
Order of \(5 = 6\)
Order of \(6 = 2\) A3
Note: Award A2 for 1 error, A1 for 2 errors, A0 for more than 2 errors.
(ii) \(\left\{ {1,\left. 6 \right\}} \right.\) ; \(\left\{ {1,\left. {2,4} \right\}} \right.\) A1A1
[6 marks]
The equation is equivalent to
\(6 * x * x = 3\) M1
\(x * x = 4\)
\(x = 2\) or \(5\) A1A1
[3 marks]

