| Date | May 2011 | Marks available | 9 | Reference code | 11M.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
(i) Draw the Cayley table for the set \(S = \left\{ {0,1,2,3,4,\left. 5 \right\}} \right.\) under addition modulo six \(({ + _6})\) and hence show that \(\left\{ {S, + \left. {_6} \right\}} \right.\) is a group.
(ii) Show that the group is cyclic and write down its generators.
(iii) Find the subgroup of \(\left\{ {S, + \left. {_6} \right\}} \right.\) that contains exactly three elements.
Prove that a cyclic group with exactly one generator cannot have more than two elements.
\(H\) is a group and the function \(\Phi :H \to H\) is defined by \(\Phi (a) = {a^{ - 1}}\) , where \({a^{ - 1}}\) is the inverse of a under the group operation. Show that \(\Phi \) is an isomorphism if and only if H is Abelian.
Markscheme
(i)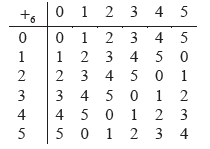
the table is closed A1
the identity is \(0\) A1
\(0\) is in every row and column once so each element has a unique inverse A1
addition is associative A1
therefore \(\left\{ {S, + \left. {_6} \right\}} \right.\) is a group R1
(ii) \(1 + 1 + 1 + 1 + 1 + 1 = 0\) M1
\(1 + 1 + 1 + 1 + 1 = 5\)
\(1 + 1 + 1 + 1 = 4\)
\(1 + 1 + 1 = 3\)
\(1 + 1 = 2\)
so \(1\) is a generator of \(\left\{ {S, + \left. {_6} \right\}} \right.\) and the group is cyclic A1
(since \(5\) is the additive inverse of \(1\)) \(5\) is also a generator A1
(iii) \(\left\{ {0,2,\left. 4 \right\}} \right.\) A1
[11 marks]
if \(a\) is a generator of group \((G, * )\) then so is \({a^{ - 1}}\) A1
if \((G, * )\) has exactly one generator \(a\) then \(a = {a^{ - 1}}\) A1
so \({a^2} = e\) and \(G = \left\{ {e,\left. a \right\}} \right.\) \(\left\{ {\left. e \right\}} \right.\) A1R1
so cyclic group with exactly one generator cannot have more than two elements AG
[4 marks]
every element of a group has a unique inverse so \(\Phi \) is a bijection A1
\(\Phi (ab) = {(ab)^{ - 1}} = {b^{ - 1}}{a^{ - 1}}\) M1A1
if \(H\) is Abelian then it follows that
\({b^{ - 1}}{a^{ - 1}} = {a^{ - 1}}{b^{ - 1}} = \Phi (a)\Phi (b)\) A1
so \(\Phi \) is an isomorphism R1
if \(\Phi \) is an isomorphism, then M1
for all \(a,b \in H\) , \(\Phi (ab) = \Phi (a)\Phi (b)\) M1
\({(ab)^{ - 1}} = {a^{ - 1}}{b^{ - 1}}\)
\( \Rightarrow {b^{ - 1}}{a^{ - 1}} = {a^{ - 1}}{b^{ - 1}}\) A1
so \(H\) is Abelian R1
[9 marks]
Examiners report
(a)(i) This was routine start to the question, but some candidates thought that commutativity was necessary as a group property.
(ii) Showing why 1 and 5 were generators would have been appropriate since this is needed for the cyclic property of the group.
(ii) This did not prove difficult for most candidates.
There were some long, confused arguments that did not lead anywhere. Candidates often do not appreciate the significance of "if" and "only".
There were some long, confused arguments that did not lead anywhere. Candidates often do not appreciate the significance of "if" and "only".

