| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.hl.TZ0.5 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
Jim is investigating the relationship between height and foot length in teenage boys.
A sample of 13 boys is taken and the height and foot length of each boy are measured.
The results are shown in the table.
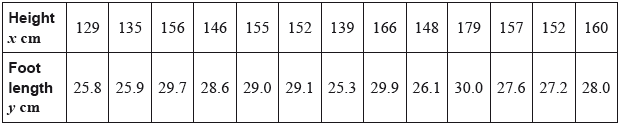
You may assume that this is a random sample from a bivariate normal distribution.
Jim wishes to determine whether or not there is a positive association between height and foot length.
Calculate the product moment correlation coefficient.
Find the \(p\)-value.
Interpret the \(p\)-value in the context of the question.
Find the equation of the regression line of \(y\) on \(x\).
Estimate the foot length of a boy of height 170 cm.
Markscheme
Note: In all parts accept answers which round to the correct 2sf answer.
\(r = 0.806\) A2
\(4.38 \times {10^{ - 4}}\) A2
\(p\)-value represents strong evidence to indicate a (positive) association between height and foot length A1
Note: FT the \(p\)-value
\(y = 0.103x + 12.3\) A2
attempted substitution of \(x = 170\) (M1)
\(y = 29.7\) A1
Note: Accept \(y = 29.8\)
Examiners report
Solutions to this question were often disappointing. Candidates were expected to use appropriate software on their calculators to do the whole question. However, some candidates used their calculators just to evaluate sums and sums of squares and then used the appropriate formulae to calculate the correlation coefficient, the p-value (which required the evaluation of the t-value first) and the equation of the regression line. This was a time consuming exercise and introduced the possibility of arithmetic error.
Solutions to this question were often disappointing. Candidates were expected to use appropriate software on their calculators to do the whole question. However, some candidates used their calculators just to evaluate sums and sums of squares and then used the appropriate formulae to calculate the correlation coefficient, the p-value (which required the evaluation of the t-value first) and the equation of the regression line. This was a time consuming exercise and introduced the possibility of arithmetic error.
Solutions to this question were often disappointing. Candidates were expected to use appropriate software on their calculators to do the whole question. However, some candidates used their calculators just to evaluate sums and sums of squares and then used the appropriate formulae to calculate the correlation coefficient, the p-value (which required the evaluation of the t-value first) and the equation of the regression line. This was a time consuming exercise and introduced the possibility of arithmetic error.
Solutions to this question were often disappointing. Candidates were expected to use appropriate software on their calculators to do the whole question. However, some candidates used their calculators just to evaluate sums and sums of squares and then used the appropriate formulae to calculate the correlation coefficient, the p-value (which required the evaluation of the t-value first) and the equation of the regression line. This was a time consuming exercise and introduced the possibility of arithmetic error.
Solutions to this question were often disappointing. Candidates were expected to use appropriate software on their calculators to do the whole question. However, some candidates used their calculators just to evaluate sums and sums of squares and then used the appropriate formulae to calculate the correlation coefficient, the p-value (which required the evaluation of the t-value first) and the equation of the regression line. This was a time consuming exercise and introduced the possibility of arithmetic error.

