| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.hl.TZ0.4 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Draw | Question number | 4 | Adapted from | N/A |
Question
A simple graph \(G\) is represented by the following adjacency table.
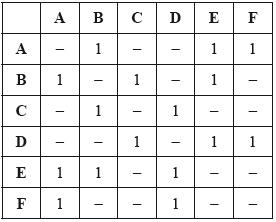
Draw the simple graph \(G\).
Explain why \(G\) does not contain an Eulerian circuit.
Show that \(G\) has a Hamiltonian cycle.
State whether or not \(G\) is planar, giving a reason for your answer.
State whether or not the simple graph \(G\) is bipartite, giving a reason for your answer.
Draw the complement \(G'\) of \(G\).
Markscheme
A1
because it has vertices which are not of even degree. A1
for example \({\text{D}} \to {\text{C}} \to {\text{B}} \to {\text{E}} \to {\text{A}} \to {\text{F}} \to {\text{D}}\) A2
\(G\) is planar. A1
either note from original graph in part (a) that there are no edges crossing or a redrawing with statement that there are no edges crossing. R1
Note: Do not accept an argument based on \(e \leqslant 3v - 6\)
the graph is not bipartite. A1
EITHER
the graph contains a triangle R1
OR
to be bipartite according to line 1 of the table A, C and D need to be one set as A connects to B, E and F. Since C and D are connected, this is contradicted. R1
A2
Note: Award A1 if extra line seen or missed out.
Examiners report
This question was very well answered in general.
This question was very well answered in general.
This question was very well answered in general.
This question was very well answered in general. In (d), some candidates stated that G is planar because \(e \leqslant 3v - 6\). It is however important to realise that this condition is necessary for a graph to be planar but not sufficient. Some candidates stated that G is planar ‘because I have drawn it as a planar graph’ or even ‘see graph in (a)’. Candidates were expected to state that G is planar because it can be drawn with no edges crossing.
This question was very well answered in general.
This question was very well answered in general.

