| Date | May 2014 | Marks available | 14 | Reference code | 14M.2.hl.TZ0.7 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find and Show that | Question number | 7 | Adapted from | N/A |
Question
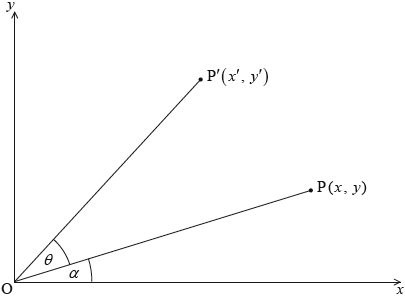
The diagram above shows the points \({\text{P}}(x,{\text{ }}y)\) and \({\rm{P'}}(x',{\text{ }}y')\) which are equidistant from the origin \({\text{O}}\). The line \(({\text{OP}})\) is inclined at an angle \(\alpha \) to the x-axis and \({\rm{P\hat OP'}} = \theta \).
(a) (i) By first noting that \({\text{OP}} = x\sec \alpha \), show that \(x' = x\cos \theta - y\sin \theta \) and find a similar expression for \(y'\).
(ii) Hence write down the \(2 \times 2\) matrix which represents the anticlockwise rotation about \({\text{O}}\) which takes \({\text{P}}\) to \({\text{P'}}\).
(b) The ellipse \(E\) has equation \(5{x^2} + 5{y^2} - 6xy = 8\).
(i) Show that if \(E\) is rotated clockwise about the origin through \(45^\circ\), its equation becomes \(\frac{{{x^2}}}{4} + {y^2} = 1\).
(ii) Hence determine the coordinates of the foci of \(E\).
Markscheme
(a) (i) \(x' = x\sec \alpha \cos (\theta + \alpha )\) M1
\( = x\sec \alpha (\cos \theta \cos \alpha - \sin \theta \sin \alpha )\) A1
\( = x\cos \theta - x\tan \alpha \sin \theta \) A1
\( = x\cos \theta - y\sin \theta \) AG
\(y' = x\sec \alpha \sin (\theta + \alpha )\) M1
\( = x\sec \alpha (\sin \theta \cos \alpha + \cos \theta \sin \alpha )\) A1
\( = x\sin \theta + x\tan \alpha \cos \theta \)
\( = x\sin \theta + y\cos \theta \) A1
(ii) the matrix \(\left[ {\begin{array}{*{20}{c}}{\cos \theta }&{ - \sin \theta }\\{\sin \theta }&{\cos \theta }\end{array}} \right]\) represents the rotation A1
[7 marks]
(b) (i) the above relationship can be written in the form
\(\left[ \begin{array}{l}x\\y\end{array} \right] = \left[ {\begin{array}{*{20}{c}}{\cos \theta }&{\sin \theta }\\{ - \sin \theta }&{\cos \theta }\end{array}} \right]\left[ \begin{array}{l}{x'}\\{y'}\end{array} \right]\) M1
let \(\theta = - \frac{\pi }{4}\)
\(x = \frac{{x'}}{{\sqrt 2 }} - \frac{{y'}}{{\sqrt 2 }}\) A1
\(y = \frac{{x'}}{{\sqrt 2 }} + \frac{{y'}}{{\sqrt 2 }}\)
substituting in the equation of the ellipse,
\(5{\left( {\frac{{x'}}{{\sqrt 2 }} - \frac{{y'}}{{\sqrt 2 }}} \right)^2} + 5{\left( {\frac{{x'}}{{\sqrt 2 }} + \frac{{y'}}{{\sqrt 2 }}} \right)^2} - 6\left( {\frac{{x'}}{{\sqrt 2 }} - \frac{{y'}}{{\sqrt 2 }}} \right)\left( {\frac{{x'}}{{\sqrt 2 }} + \frac{{y'}}{{\sqrt 2 }}} \right) = 8\) M1
\(5\left( {\frac{{{{x'}^2}}}{2} + \frac{{{{y'}^2}}}{2} - x'y'} \right) + 5\left( {\frac{{{{x'}^2}}}{2} + \frac{{{{y'}^2}}}{2} + x'y'} \right) - 6\left( {\frac{{{{x'}^2}}}{2} - \frac{{{{y'}^2}}}{2}} \right) = 8\) A1
leading to \(\frac{{{{x'}^2}}}{4} + {y'^2} = 1\) AG
Note: Award M1A0M1A0 for using \(\theta = \frac{\pi }{4}\) leading to \(\frac{{{{y'}^2}}}{4} + {x'^2} = 1\).
(ii) in the usual notation, \(a = 2\), \(b = 1\) (M1)
the coordinates of the foci of the rotated ellipse are \(\left( {\sqrt {3,} {\text{ 0}}} \right)\) and \(\left( { - \sqrt {3,} {\text{ 0}}} \right)\) A1
the coordinates of the foci of \({\text{E}}\) are therefore \(\left( {\frac{{\sqrt 3 }}{{\sqrt 2 }},{\text{ }}\frac{{\sqrt 3 }}{{\sqrt 2 }}} \right)\) and \(\left( {\frac{{ - \sqrt 3 }}{{\sqrt 2 }},{\text{ }}\frac{{ - \sqrt 3 }}{{\sqrt 2 }}} \right)\) A1
[7 marks]

