| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.sl.TZ1.6 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
A lobster trap is made in the shape of half a cylinder. It is constructed from a steel frame with netting pulled tightly around it. The steel frame consists of a rectangular base, two semicircular ends and two further support rods, as shown in the following diagram.
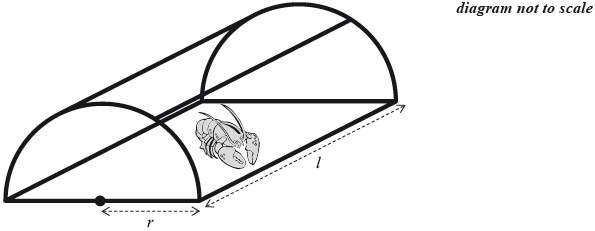
The semicircular ends each have radius \(r\) and the support rods each have length \(l\).
Let \(T\) be the total length of steel used in the frame of the lobster trap.
Write down an expression for \(T\) in terms of \(r\), \(l\) and \(\pi \).
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Write down an equation for the volume of the lobster trap in terms of \(r\), \(l\) and \(\pi \).
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Show that \(T = (2\pi + 4)r + \frac{6}{{\pi {r^2}}}\).
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Find \(\frac{{{\text{d}}T}}{{{\text{d}}r}}\).
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Show that the value of \(r\) for which \(T\) is a minimum is \(0.719 {\text{ m}}\), correct to three significant figures.
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Calculate the value of \(l\) for which \(T\) is a minimum.
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Calculate the minimum value of \(T\).
Markscheme
\(2\pi r + 4r + 4l\) (A1)(A1)(A1)
Notes: Award (A1) for \(2\pi r\) (“\(\pi \)” must be seen), (A1) for \(4r\), (A1) for \(4l\). Accept equivalent forms. Accept \(T = 2\pi r + 4r + 4l\). Award a maximum of (A1)(A1)(A0) if extra terms are seen.
[3 marks]
\(0.75 = \frac{{\pi {r^2}l}}{2}\) (A1)(A1)(A1)
Notes: Award (A1) for their formula equated to \(0.75\), (A1) for \(l\) substituted into volume of cylinder formula, (A1) for volume of cylinder formula divided by \(2\).
If “\(\pi \)” not seen in part (a) accept use of \(3.14\) or greater accuracy. Award a maximum of (A1)(A1)(A0) if extra terms are seen.
[3 marks]
\(T = 2\pi r + 4r + 4\left( {\frac{{1.5}}{{\pi {r^2}}}} \right)\) (A1)(ft)(A1)
\( = (2\pi + 4)r + \frac{6}{{\pi {r^2}}}\) (AG)
Notes: Award (A1)(ft) for correct rearrangement of their volume formula in part (b) seen, award (A1) for the correct substituted formula for \(T\). The final line must be seen, with no incorrect working, for this second (A1) to be awarded.
[2 marks]
\(\frac{{{\text{d}}T}}{{{\text{d}}r}} = 2\pi + 4 - \frac{{12}}{{\pi {r^3}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi + 4\), (A1) for \(\frac{{ - 12}}{\pi }\), (A1) for \({r^{ - 3}}\).
Accept 10.3 (10.2832…) for \(2\pi + 4\), accept \(–3.82\) \(–3.81971…\) for \(\frac{{ - 12}}{\pi }\). Award a maximum of (A1)(A1)(A0) if extra terms are seen.
[3 marks]
\(2\pi + 4 - \frac{{12}}{{\pi {r^3}}} = 0\) OR \(\frac{{{\text{d}}T}}{{{\text{d}}r}} = 0\) (M1)
Note: Award (M1) for setting their derivative equal to zero.
\(r = 0.718843 \ldots \) OR \(\sqrt[3]{{0.371452 \ldots }}\) OR \(\sqrt[3]{{\frac{{12}}{{\pi (2\pi + 4)}}}}\) OR \(\sqrt[3]{{\frac{{3.81971}}{{10.2832 \ldots }}}}\) (A1)
\(r = 0.719{\text{ (m)}}\) (AG)
Note: The rounded and unrounded or formulaic answers must be seen for the final (A1) to be awarded. The use of \(3.14\) gives an unrounded answer of \(r = 0.719039 \ldots \).
[2 marks]
\(0.75 = \frac{{\pi \times {{(0.719)}^2}l}}{2}\) (M1)
Note: Award (M1) for substituting \(0.719\) into their volume formula. Follow through from part (b).
\(l = 0.924{\text{ (m)}}\) \((0.923599 \ldots )\) (A1)(ft)(G2)
[2 marks]
\(T = (2\pi + 4) \times 0.719 + \frac{6}{{\pi {{(0.719)}^2}}}\) (M1)
Notes: Award (M1) for substituting \(0.719\) in their expression for \(T\). Accept alternative methods, for example substitution of their \(l\) and \(0.719\) into their part (a) (for which the answer is \(11.08961024\)). Follow through from their answer to part (a).
\( = 11.1{\text{ (m)}}\) \((11.0880 \ldots )\) (A1)(ft)(G2)

